Определение определенного интеграла

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Лекция 6

Дополнительная

Основная

СПИСОК ЛИТЕРАТУРЫ

Вопросы для самоконтроля

Интегрирование некоторых иррациональных функций.

Интеграл вида где n- натуральное число.

С помощью подстановки 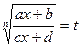функция рационализируется.

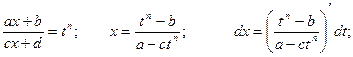
Тогда

1. Какие методы интегрирования Вы знаете?

2. Как находятся интегралы от элементарных дробей?

2. Как находятся интегралы от рациональных функций?

3. Как находятся интегралы от тригонометрических функций?

4. Как находятся интегралы от иррациональных функций?

1. Дмитрий Письменный, Конспект лекций по высшей математике. М., АЙРИС ПРЕСС,2007.600с.

2. Данко П.Е., Попов Л.Г., Кожевникова Т.Е., Данко С.И. Высшая математика в упражнениях и задачах. 2006.-187с. ООО Изд. Мир и образование.

1. Зайцев И.А, Высшая математика, М, Высшая школа, 1991, 400с,

2. Кудрявцев В.А., Демидович Б.П, Краткий курс высшей математики. М., Наука, 1984. 624с.

Пусть на отрезке [a, b] задана непрерывная функция f(x).

Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками.

x₀ < x₁ < x₂ < … < x_n

Тогда x₁ – x₀ = Dx₁, x₂ – x₁ = Dx₂, …,x_n – x_n-1 = Dx_n;

Внутри каждого отрезка выберем некоторую точку e.

x₀ < e₁ < x₁, x₁ < e < x₂, …, x_n-1 < e < x_n.

Обозначим maxDx_i – наибольший отрезок разбиения, то число отрезков разбиения отрезка [a, b] стремится к бесконечности.

Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDx_i® 0 и произвольном выборе точек e_i интегральная сумма 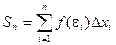стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].

Обозначение: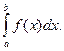

а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.

Определение: Если для функции f(x) существует предел то функция называется интегрируемой на отрезке [a, b].

Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.

Дата добавления: 2013-12-13