Определение и вычисление несобственных интегралов

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

Лекция 7

Дополнительная

Основная

СПИСОК ЛИТЕРАТУРЫ

Вопросы для самоконтроля

1. Что такое определенный интеграл?

2. Какими свойствами обладает определенный интеграл?

3. Как вычисляются определенные интегралы?

1. Дмитрий Письменный, Конспект лекций по высшей математике. М., АЙРИС ПРЕСС,2007.600с.

2. Данко П.Е., Попов Л.Г., Кожевникова Т.Е., Данко С.И. Высшая математика в упражнениях и задачах. 2006.-187с. ООО Изд. Мир и образование.

1. Зайцев И.А, Высшая математика, М, Высшая школа, 1991, 400с,

2. Кудрявцев В.А., Демидович Б.П, Краткий курс высшей математики. М., Наука, 1984. 624с.

Пусть функция f(x) определена и непрерывна на интервале [a, ¥). Тогда она непрерывна на любом отрезке [a, b].

Определение: Если существует конечный предел , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).

Обозначение: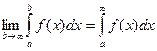

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

Аналогичные рассуждения можно привести для несобственных интегралов вида:

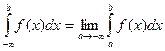
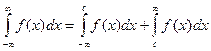
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.

Теорема: Если для всех х (x ³ a) выполняется условие и интеграл 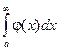сходится, то 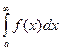тоже сходится и 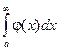³ .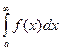

Теорема: Если для всех х (x ³ a) выполняется условие 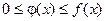и интеграл 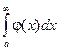расходится, то 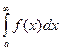тоже расходится.

Теорема: Если 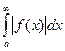сходится, то сходится и интеграл .

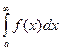В этом случае интеграл 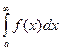называется абсолютно сходящимся.

Дата добавления: 2013-12-13