Основная. Приближенное вычисление определенного интеграла

СПИСОК ЛИТЕРАТУРЫ

Вопросы для самоконтроля

Формула парабол

Формула трапеций.

Приближенное вычисление определенного интеграла.

Как было сказано выше, существует огромное количество функций, интеграл от которых не может быть выражен через элементарные функции. Для нахождения интегралов от подобных функций применяются разнообразные приближенные методы, суть которых заключается в том, что подинтегральная функция заменяется “близкой” к ней функцией, интеграл от которой выражается через элементарные функции.

Формула прямоугольников.

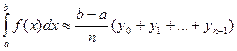или

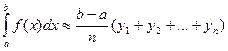- любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников.

Эта формула является более точной по сравнению с формулой прямоугольников.

Подинтегральная функция в этом случае заменяется на вписанную ломаную.

Формула трапеций имеет вид:

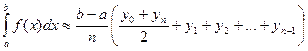
(формула Симпсона или квадратурная формула).

Разделим отрезок интегрирования [a, b] на четное число отрезков (2m). Площадь криволинейной трапеции, ограниченной графиком функции f(x) заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси Оу и проходящей через точки кривой, со значениями f(x₀), f(x₁), f(x₂).

Получаем формулу Симпсона:

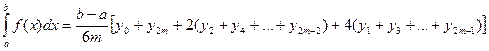
Чем больше взять число m, тем более точное значение интеграла будет получено.

1. Что такое несобственный интеграл?

2 как вычисляется несобственный интеграл?

3. Как можно приближенно вычислить определенный интеграл?

1. Дмитрий Письменный, Конспект лекций по высшей математике. М., АЙРИС ПРЕСС,2007.600с.

2. Данко П.Е., Попов Л.Г., Кожевникова Т.Е., Данко С.И. Высшая математика в упражнениях и задачах. 2006.-187с. ООО Изд. Мир и образование.

Дата добавления: 2013-12-13