Основная. Определение. Пусть точка М0(х0, у0) принадлежит области определения функции f(x, y)

СПИСОК ЛИТЕРАТУРЫ

Вопросы для самоконтроля

Непрерывность.

Определение. Пусть точка М₀(х₀, у₀) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется непрерывной в точке М₀(х₀, у₀), если 1)функция z = f(x, y) определена в точке М₀(х₀, у₀); 2) существует предел 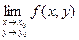; 3)этот предел равен значению функции в точке М₀(х₀, у₀). Обозначение: ,

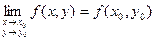причем точка М(х, у) стремится к точке М₀(х₀, у₀) произвольным образом.

Если в какой – либо точке одно из условий не выполняется, то эта точка называется точкой разрыва функции f(x, y). Это может быть в следующих случаях.

1) Функция z = f(x, y) не определена в точке М₀(х₀, у₀).

2) Не существует предел .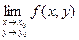

3) Этот предел существует, но он не равен f(x₀, y₀).

Определение. Функция f(x, y), непрерывная в замкнутой ограниченной области D, называется ограниченной в этой области, если существует такое число М, что для всех точек области верно неравенство .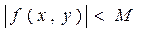

Определение. Если функция f(x, y) определена и непрерывна в замкнутой ограниченной области D, то она называется равномерно непрерывной в этой области, т.е. для любого положительного числа e существует такое число D > 0, что для любых двух точек (х₁, y₁) и (х₂, у₂) области, находящихся на расстоянии, меньшем D, выполнено неравенство: .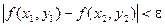

1. Что такое функции нескольких переменных?

2. Что такое предел функции двух переменных?

3. Какие функции называются непрерывными?

1. Дмитрий Письменный, Конспект лекций по высшей математике. М., АЙРИС ПРЕСС,2007.600с.

2. Данко П.Е., Попов Л.Г., Кожевникова Т.Е., Данко С.И. Высшая математика в упражнениях и задачах. 2006.-187с. ООО Изд. Мир и образование.

Дата добавления: 2013-12-13