Технологии производства в экономико-математических моделях

Введем следующую систему оборзначений:

i-индекс пункта производства, i=1,2,….m;

j- индекс пункта потребления, j=1,2,..n;

ai – максимально возможная мощность в i-м пункте производства;

bj - потребность j-го пункта потребления;

tij – затраты на перевозку единицы продукта из i-го пункта производства в j-й пункт потребления;

si – затраты на производство единицы продукта в i-м пункте нового строительства(расширения или реконструекции действующего предприятия);

xij- объем первозок из i-го пункта производства в j-й пункт потребления;

xi- размер производства в i-м пункте производства.

Требуется найти значение величин Xij и Xi, минимизирующих суммарный объем затрат на производство и доставку продукции

При выполнении следующих условий:

Суммарный ввоз продукции в каждый из пунктов потребления должен быть равен его потребностям

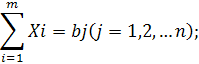
Суммарный вывоз продукции из каждого пункта производства должен быть равен размеру производства, а последний, в свою очередь, не может превосходить маскимально возможный предел

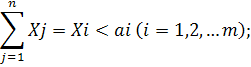
Объем перевозок по всем возможным коммуникациям и размеры производства в каждом из пунктов должены быт неортицательны

Xij>=0, (i=1,2,…m; j=1,2,..n)

Xi>=0,(i=1,2,…m)

Перепишим критерий оптимальности

Или проведем несложные преобразования

Иными словами, искомые в процессе решения перспективные производственные мощности предприятия могут принимать не любые значения на всем интервале измененияч мощности(непрерывность), а лишь некоторые, строго определеннвые значения, т.е. в этом случае имеем задачу развития и размещения с дискретными(целочисленными) переменными.

Дата добавления: 2014-01-04