Модель управления производственными запасами с учетом спроса и цен на продукцию

Определим функцию изменения запаса, т.е. связь между количеством единиц товара на складе (обозначим его через Q) и временем t. Будем считать, что имеется один вид товара.

Если на товар имеется спрос, то функция изменения запаса Q = Q(t) убывает. Если товар, наоборот, завозят на склад, то эта функция возрастает.

Затраты, связанные с запасами, можно разделить на три части.

· Стоимость товара.

· Организационные издержки. Это расходы, связанные с оформлением товара, его доставкой, разгрузкой и т. д.

· Издержки на хранение товара. Это затраты на аренду склада, амортизацию в процессе хранения и т. д.

Рассмотрим основные величины и предположения, принятые в рамках основной модели.

1. Цена единицы товара примим с у.е. Цена постоянна, рассматривается один вид товара.

2. Интенсивность спроса примим d единиц товара в год. Будем считать, что спрос постоянный и непрерывный.

3. Организационные издержки примим s у.е.═ за одну партию товара. Будем считать, что организационные издержки не зависят от размера поставки, т. е. от количества единиц товара в одной партии.

4. Издержки на хранение запаса примим h у.е.═ на единицу товара в год. Будем считать эти издержки постоянными.

5. Размер одной партии товара постоянен примим q единиц. Партия поступает мгновенно в тот момент, когда возникает дефицит, т. е. когда запас на складе становится равным нулю.

При сделанных предположениях график функции изменения запаса будет таким, как показано на рис. 2: он состоит из повторяющихся циклов пополнения запаса между двумя соседними дефицитами. Вертикальные отрезки отвечают мгновенному пополнению запаса.

Параметры с, d, s, h считаются заданными. Задача управления запасами состоит в выборе параметра q таким образом, чтобы минимизировать годовые затраты.

Для решения сформулированной задачи надо прежде всего выразить эти затраты через параметры с, d, s, h, q.

1. Поскольку годовая интенсивность спроса равна d, а цена единицы товара примим с, то общая стоимость товара в год равна cd.

2. Поскольку в одной партии q единиц товара, а годовой спрос равен d, то число поставок равно d/q. В течение года организационные издержки равны*S

3. Средний уровень запаса равен отношению площади под графиком за цикл к продолжительности цикла. Этот средний уровень равен q/2 (на рис. 2 обозначен пунктиром). Поскольку годовые издержки на хранение единицы товара равны h, то общие издержки на хранение составляют *h

Рисунок 2. Уровень запаса

Таким образом, общие издержки С вычисляются по формуле

С=c*d++.

Требуется найти такое число q*, чтобы функция С = C(q) принимала наименьшее значение на множестве q > 0 именно в точке q*.

График функции С = C(q) показан на рис. 2.

Для нахождения точки q* минимума функции С = C(q) найдем ее производную (с, d, s, h примим фиксированные числа):

С”(q)=(cd)’+)’= -+.

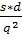Приравнивая C'(q) к нулю, получаем

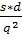-+=0.

Отсюда можно найти q*. Имеем:

q*=.

Полученная формула называется формулой оптимального запаса или формулой Харриса (Harris).

Дата добавления: 2014-01-04