Метод обратной матрицы и метод Крамера

Рассмотрим частный случай системы (3), когда число уравнений равно числу неизвестных, т.е. 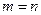. Система уравнений имеет вид:

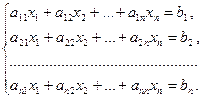(5)

Составим квадратную матрицу А порядка 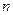этой системы:

. (6)

В матричной форме система уравнений (5) имеет вид:

где матрицы 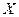и 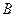имеют размер 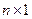. Пусть матрица системы является невырожденной, т.е. существует обратная матрица 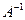. Умножив обе части этого уравнения слева на 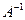, получаем 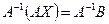, используя свойства произведения матриц получаем 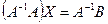, откуда 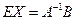и решением системы методом обратной матрицы будет матрица-столбец

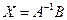(7)

Когда порядок матриц и 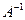достаточно велик, вычисление обратной матрицы может быть очень громоздким.

Другой метод решения системы уравнений (5) основан на теореме Крамера (Габриэль Крамер (1704-1752) швейцарский математик)).

Рассмотрим решение системы двух уравнений с двумя переменными

(8)

в которой хотя бы один из коэффициентов при переменных отличен от нуля. Для решения этой системы исключим переменную , умножив первое уравнение системы на , а второе – на 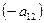и сложив их. Затем исключим переменную , умножив первое уравнение системы на , а второе – на 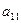и также сложив их. В результате получим систему

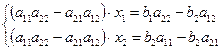(9)

Выражение в скобках есть определитель системы

Обозначим ; 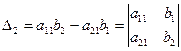, тогда система (7) примет вид

(10)

Из полученной системы следует, что если определитель системы , то система (8) имеет единственное решение, определяемое по формулам: .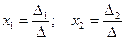

Если определитель системы , а (или 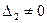), то система (8) несовместная, так как в этом случае она приводится к виду:

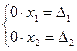
Если определитель системы , то система (8) неопределенная, так как в этом случае она приводится к виду:

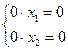
Вернемся к системе линейных уравнений (5). Составим определитель матрицы А:

,

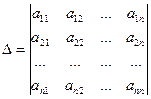который называется определителем системы. Заменим в этом определителе 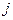-й столбец на столбец свободных членов 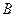, т.е. получим этой заменой другой определитель, который обозначим :

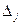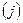
Теорема (правило Крамера). Пусть - определитель матрицы системы , а 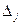- определитель, полученный из определителя заменой 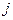-ого столбца на столбец свободных членов 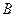. Тогда, если , то система линейных уравнений (5) имеет единственное решение, определяемое по формулам

, .

Ранее мы фактически получили формулы Крамера в частном случае при решении системы (8) – системы двух уравнений с двумя переменными.

Дата добавления: 2014-01-05