Специфіка філософського знання. 1 страница

2

L

T

T

Додаток 2

СПІВВІДНОШЕННЯ ОЦІНОК ЗНАНЬ ЗА НАЦІОНАЛЬНОЮ ШКАЛОЮ, ШКАЛОЮ ECTS ТА ШКАЛОЮ НАВЧАЛЬНОГО ЗАКЛАДУ

За шкалою ECTS	За національною шкалою	За шкалою навчального закладу
А	5 (відмінно)	90-100
В,С	4(добре)	75-89
D,Е	3(задовільно)	60-74
FХ	2 (незадовільно з можливістю повторного складання)	35-59
F	2 (незадовільно з обов’язковим повторним курсом)	1-34

ЗМІСТ

Передмова.............................................................................................................

Лекція 1. Культура мови як складова частина загальнолюдської культури...

Лекція 2.Статус і становлення української мови як державної.....................

Лекція 3. Норми сучасної української літературної мови..............................

Лекція 4.Функціональні стилі сучасної української літературної мови......

Лекція 5. Писемне ділове мовлення.................................................................

Лекція 6. Словникова справа в Україні............................................................

Лекція 7.Культура терміновживання і термінотворення...............................

Лекція 8. Усне ділове мовлення........................................................................

Лекція 9. Мовленнєвий етикет – невід’ємний елемент культури

мовлення.............................................................................................

Теми для самостійної роботи студентів..........................................................

Практичні завдання до курсу...........................................................................

Варіанти завдань для контрольних робіт........................................................

Методичні вказівки щодо оформлення та написання реферату..................

Тематика рефератів..........................................................................................

Додаток 1. Система критеріїв оцінювання знань.........................................

Додаток 2. Співвідношення оцінок знань за національною шкалою,

шкалою ECTS та шкалою навчального закладу........................................

t

T

3 Т

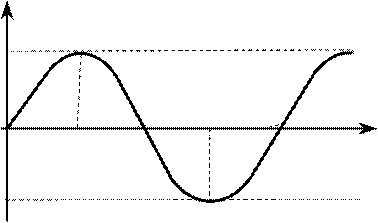4

λ = VT

Рис. 4

= V

Довжина хвилі ν

, де Т – період; ν – частота хвилі.

Зв’язок різниці фаз ∆φ коливань з відстанню ∆х між точками середовища, що відраховані в напрямку розповсюдження коливань:

2π

∆φ =

λ

∆х.

1.2. Основні закони динаміки

Перший закон Ньютона

Матеріальна точка (тіло) зберігає стан спокою або прямолі-

нійного рівномірного руху, якщо на неї не діють інші тіла, або їх дія скомпенсована. Цей стан – це рух за інерцією.

Перший закон Ньютона постулює існування інерціальних сис-

тем відліку. Інерціальна система відліку повинна бути зв’язана з не- взаємодіючим тілом відліку, тобто з тілом, що рухається рівномірно і прямолінійно. Будь яка інша система відліку, що рухається відносно установленої інерціальної системи відліку рівномірно і прямолінійно,

або знаходиться в спокої – теж інерціальна.

Повний клас ІСВ можна одержати з даної інерціальної системи відліку перенесенням її початку відліку, поворотами осей координат,

або рівномірним поступальним рухом системи координат (група перетворень Галілея).

Неінерціальну систему відліку визначають як таку систему, що зв’язана з тілом відліку, яке рухається з прискоренням. Інерціальна система відліку – це абстракція. Реальні системи відліку тим ближче

наближаються до ІСВ, чим менше прискорення, з яким рухається тіло відліку реальної системи. Вибір ІСВ відбувається дослідним шляхом:

1) система відліку, зв’язана з поверхнею Землі – геоцентрична (лабораторна) система відліку – є наближено інерціальною для великого кола явищ, в яких можна знехтувати добовим обертанням Землі навколо власної осі та обертанням навколо Сонця;

2) система відліку, зв’язана з центром Сонця, в якій осі коор-

динат направлені на три відомі зірки – геліоцентрична система відліку – є зі значно більшою точністю інерціальною системою відліку.

Масою m тіла називається скалярна фізична величина, яка є мірою інерційних властивостей тіла при його поступальному русі.

Імпульсом Р матеріальної точки називається векторна фізич- на величина, яка дорівнює добутку маси матеріальної точки на її швидкість:

Другий закон Ньютона

Р = mVr.

Швидкість зміни імпульсу матеріальної точки дорівнює діючій на неї силі:

r

dP

dt = F.

Якщо на матеріальну точку одночасно діють декілька сил, то згідно з принципом незалежності дії сил, F є рівнодійною прикладених сил.

Якщо масу тіла вважати постійною, то другий закон Ньютона можна записати так:

прискорення матеріальної точки прямо пропорційно діючій на неї силі та обернено пропорційно її масі:

v

av = F

m.

Зазначимо, що другий закон Ньютона справедливий тільки в інерціальних системах відліку.

Третій закон Ньютона

Сили взаємодії між двома матеріальними точками (тілами)

рівні за величиною, протилежні за напрямком і направлені вздовж прямої, що з'єднує ці матеріальні точки.

F

r = − Fr.

F

r r

Звернемо увагу, що сили F 1

і 2 прикладені до різних

матеріальних точок (тіл), тому ніколи не врівноважують одна одну.

Другий і третій закони Ньютона дають змогу розглядати рух не тільки окремих тіл (матеріальних точок), але й механічних систем. Механічна система тіл, на яку не діють зовнішні сили, називається

замкненою (або ізольованою).

Закон збереження імпульсу

Імпульс замкненої системи є величина постійна:

r n r n r

P = ∑ Pi

i=1

= ∑ miVi

i=1

= const,

деPr − імпульссистеми, якийдорівнюєвекторнійсуміімпульсіввсіх

тіл системи; n – кількість тіл, що утворюють замкнену систему.

Сили, які розглядаються в механіці:

а) гравітаційна сила F, яка визначається за законом всесвітнього тяжіння:

-11

G

де = 6,67·10

2 2

Н·м /кг

F = G m1m2,

r 2

– гравітаційна стала; m1, m2 – маси матері-

r – відстань між ними.

альних точок, між якими діє сила притягання;

Гравітаційні сили є силами притягання і направлені вздовж прямої, що з’єднує ці матеріальні точки, тобто є центральними.

Одним із проявів дії таких сил є сила тяжіння – сила, з якою

Земля притягує до себе тіла.

F = mgr,

де gr − прискорення вільного падіння;

б) сила пружності виникає при пружних деформаціях і визначається за законом Гука:

F = - kх,

де k – коефіцієнт пружності; х – абсолютна деформація; знак „- „

показує, що сила направлена протилежно напрямку деформації. Цей закон записується також у вигляді:

σ = Еε,

F

де σ =

S

− механічне напруження; Е – модуль Юнга (є

деформаційною характеристикою даного матеріалу); ε − відносна деформація;

в) сила тертя (зовнішнього) – сила, що виникає на поверхні двох твердих тіл, що контактують, і спрямована по дотичній до поверхні контакту в бік, протилежний руху тіла. Зовнішнє (сухе) тертя виникає при відносному переміщенні двох поверхонь твердих тіл, що контактують (тертя ковзання, кочення) або при спробах викликати

таке переміщення (тертя спокою). Сила тертя ковзання дорівнює:

F = µΝ,

де µ – коефіцієнт тертя ковзання; Ν – сила нормального тиску.

1.3. Робота та енергія.

Кінетична і потенціальна енергія. Повна механічна енергія

Енергією називається скалярна фізична величина, яка є універсальною кількісною мірою різних форм руху матерії. Різним формам руху матерії відповідають різні види енергії. Так, механічній формі руху матерії відповідає механічна енергія, тепловій формі руху

-− теплова енергія тощо. Запас енергії характеризує здатність тіла виконувати роботу.

Робота, яку здійснює постійна сила F при переміщенні тіла на прямолінійній ділянці шляху s, визначається скалярним добутком

вектора сили Fr і вектора переміщення s точки прикладання сили.

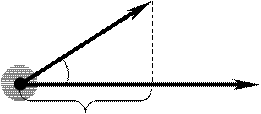F

α S

F

S

Рис.5

A=(Fr sr) = Fscosα= Fss,

де α − кут між векторами сили F і переміщення s;

проекція сили на напрямок переміщення (рис.5).

Fs = F cosα −

Робота є скалярною величиною, вона може бути позитивною, від’ємною чи рівною нулю. Самостійно проаналізуйте, коли реалізується кожний з цих випадків.

У загальному випадку руху тіла по криволінійній траєкторії під дією змінної сили Fr спочатку знаходять елементарну роботу dA на

елементарному переміщенні

dr:

dA = (Fdr) = Fr dr.

Сумарну роботу А сили F на ділянці траєкторії від точки 1 до точки 2 знаходять інтегруванням:

2 2

A = ∫dA = ∫ Fr dr.

1 1

Одиницею роботи в СІ є джоуль (Дж):

1 Дж = 1 Н ·м.

Консервативною називають силу, робота якої визначається тільки початковим і кінцевим положенням тіла на траєкторії і не залежить від форми траєкторії. Робота консервативних сил по замкненій траєкторії дорівнює нулю. Прикладом консервативних сил є сили тяжіння, сили пружності. Прикладом неконсервативних сил (дисипативних) є сили тертя (сили опору).

Фізична величина, яка дорівнює відношенню роботи dA до

,

проміжку часу dt

за який ця робота виконується, називається

потужністю:

N = dA = Fv cosα.

dt

Одиниця потужності в СІ– ват (Вт):

1Вт =1 Дж.

с

Кінетична і потенціальна енергія. Повна механічна енергія

У механіці розглядають два види енергії: кінетичну енергію Wk

(енергію руху) і потенціальну енергію Wп (енергію взаємодії).

Повна механічна енергія тіла (системи тіл) W складається із суми кінетичної і потенціальної енергій:

Wk + Wп = W.

Кінетична енергія тіла масою m, яке рухається поступально з

,

швидкістю v

визначається за формулою:

W =

mv2

k 2.

Кінетична енергія тіла, що обертається навколо нерухомої осі, визначається за формулою:

W =

Jω 2

k 2,

де J − момент інерції тіла відносно осі обертання; ω – його кутова швидкість.

Якщо тіло масою m одночасно рухається поступально і обертально, то

Wk =

де v −швидкість центра мас.

mv2

Jω 2

+,

Потенціальна енергія – це енергія системи взаємодіючих тіл (“Земля – тіло, підняте над Землею”), або системи взаємодіючих частинок окремого тіла (пружно-деформоване тіло).

Потенціальна енергія залежить від природи сил взаємодії і від конфігурації системи.

Різним видам взаємодії відповідають різні формули для потенціальної енергії. Наприклад:

1. Потенціальна енергія гравітаційної взаємодії двох матеріальних

точок, що знаходяться на відстані r:

n

W = −G m1m2.

r

2. Потенціальна енергія тіла масою m, піднятого над поверхнею Землі на висоту h (h << RЗ, поверхня Землі прийнята за нульовий рівень):

Wn = mgh.

3. Потенціальна енергія пружно-деформованої пружини:

kx2

Wn = 2,

де x − величина деформації; k − коефіцієнт пружності.

Закон збереження механічної енергії

Повна механічна енергія замкненої системи тіл, в якій діють тільки консервативні сили, є величина стала:

W = Wk + Wn = const.

1.4. Динаміка обертального руху твердого тіла

Обертальну дію сили характеризують фізичною величиною – моментом сили. Момент сили − це вектор, напрямок якого в просторі зв’язаний з обертанням – аксіальний вектор.

Моментом сили відносно нерухомої точки О називається фізична величина, що визначається векторним добутком радіуса –

вектора r, проведеного із точки О в точку А прикладання сили, на вектор сили Fr (рис. 6):

M = [rF].

Вектор моменту сили M направлений перпендикулярно до площини векторів r і Fr. Його напрямок визначається правилом

правого гвинта при його обертанні від r до F. Модуль моменту сили дорівнює добутку сили F на плече l:

M = Fr sin α

= Fl,

де α – гострий кут між векторами r і F; l = rsinα – найкоротша відстань між лінією дії сили і і точкою О – плече сили.

Моментом сили відносно нерухомої осі Z називається скалярна величина Мz, яка дорівнює проекції на цю вісь вектора

моменту сили М, визначеного відносно довільної точки О, вибраної на цій осі (рис.7).

M Z

M

M

Z Fr

0 F

r

l 90o α

A

0 r A

Рис. 6

Рис. 7

Мірою інертності тіла при обертальному русі є динамічна характеристика обертання – момент інерції J.

Моментом інерції тіла (система матеріальних точок) відносно

даної осі називається фізична скалярна величина, яка дорівнює сумі моментів інерції всіх матеріальних точок, з яких складається тіло:

J = ∑ Ji

i=n

= ∑ miri,

i=1

деJ

= m r 2 − моментінерціїматеріальноїточкивідносноданоїосі.

i i i

У випадку неперервного розподілу маси в тілі ця сума зводиться до інтеграла:

J = ∫ r 2dm,

де інтегрування виконується по всьому об’єму тіла.

Наведемо приклади моментів інерцій деяких однорідних тіл правильної геометричної форми (вісь обертання проходить через центр мас).

1.Момент інерції матеріальної точки (рис.8):

J = m r.

m r

Рис.8

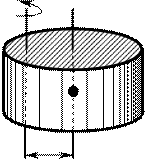
2. Момент інерції обруча (тонкостінного порожнинного циліндра) відносно осі, що проходить перпендикулярно площині обруча в центрі кола (вісь збігається з віссю циліндра):

J = mr 2, де r – радіус обруча (циліндра).

3. Момент інерції однорідного диска (або циліндра) радіусом r

відносно осі, яка перпендикулярна площині диска (або циліндра), та збігається з геометричною віссю (віссю симетрії) (рис. 9):

r

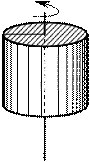m J =

1 mr 2

2.

Рис. 9

4. Момент інерції кулі (рис.10):

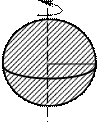m r

J = 2 mr 2

5.

Рис.10

5. Момент інерції стержня довжиною l відносно осі, що проходить перпендикулярно стержню, посередині його (рис.11):

m J =

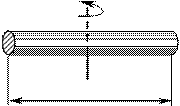l

1 ml2

12.

Рис.11

Якщо відомий момент інерції тіла відносно осі, що проходить через його центр мас, то момент інерції відносно будь якої паралель- ної осі визначається теоремою Штейнера:

момент інерції J тіла відносно довільної осі дорівнює його мо-

менту інерції Jс відносно паралельної осі, що проходить через центр мас С тіла плюс добуток маси тіла на квадрат відстані d між осями (рис.12):

O

O1

C

O1 d O

J = J c

+ md 2.

Рис.12

Основне рівняння динаміки обертального руху твердого тіла відносно нерухомої осі записується так:

M z = J z β,

де Мz – момент сили відносно осі Z; Jz − момент інерції тіла відносно осі; β= dω/dt – кутове прискорення тіла.

Якщо вісь Z збігається з головною віссю інерції тіла, яка прохо- дить через центр мас, то має місце векторна рівність:

M = Jβ.

Момент імпульсу. Закон збереження моменту імпульсу

Момент імпульсу твердого тіла Lz відносно нерухомої осі Z – фізична величина, яка дорівнює добутку моменту інерції тіла на його кутову швидкість:

Lz = J zω.

У випадку обертання тіла навколо нерухомої осі, що проходить через його центр мас, момент імпульсу обчислюється за формулою:

L = Jωr.

Введення вектора моменту імпульсу дозволяє записати основне рівняння динаміки обертального руху у більш загальній формі, подібній до рівняння Ньютона для поступального руху:

Mr =

dL

dt.

dLr

dt

Для замкненої системи момент зовнішніх сил

= 0, звідки

Мr = 0,

тоді

L = Jωr = const.

Цей вираз являє собою закон збереження моменту імпульсу.

Момент імпульсу замкненої системи є велична стала, тобто не змінюється з часом.

газу):

РОЗДІЛ 2. ОСНОВИ МОЛЕКУЛЯРНОЇ ФІЗИКИ ТА ТЕРМОДИНАМІКИ

2.1. Рівняння стану ідеального газу. Газові закони

Рівняння Мендєлєєва - Клапейрона (рівняння стану ідеального

PV = m RT M

= νRT,

де P,V,T – параметри стану; M – молярна маса; ν =m/ M –

кількість речовини; R = 8,31 Дж/моль·К – універсальна газова стала;

Т – термодинамічна температура.

Експериментальні газові закони є частинним випадком рівняння

Менделєєва – Клапейрона для ізопроцесів:

а) закон Бойля – Маріотта (ізотермічний процес, Т = const,

m = const):

рV = const, для двох станів: р1V1 = р2V2;

б) закон Гей – Люссака (ізобарний процесс, р = const, m =

const):

V V V

= const,

для двох станів: 1 = 2;

T T T

1 2

в) закон Шарля (ізохорний процес, V = const, m = const):

p = const,

T

для двох станів:

р1 = р2;

Т1 Т2

г) об’єднаний газовий закон (m = const):

pV = const,

T

або

p1V1 =

T1

p2V2

,

T2

де р1, V1, Т1 – тиск, об’єм та температура газу в початковому стані;

р2, V2, Т2 – те ж саме, в кінцевому стані.

Закон Дальтона визначає тиск суміші газів:

n

p = ∑ pi,

i =1

де рі – парціальні тиски компонентів суміші; і – число компонентів суміші.

Парціальний тиск є тиск газу, який створював би цей газ, якби

він один знаходився в ємності, яку займає суміш.

2.2. Основне рівняння молекулярно – кінетичної теорії ідеальних газів

Тиск ідеального газу р прямо пропорційний концентрації n

молекул газу і середній кінетичні енергії поступального руху

<εпост> молекули газу:

p = 3 n < ε пост

>. (1)

Відповідно до експериментальних газових законів і висновків молекулярно-кінетичної теорії газів встановлено, що

< ε >= 3 kT, (2)

пост. 2

де k = 1,38·10-23 Дж/К – стала Больцмана; Т – термодинамічна температура.

Тоді рівняння (1) можна записати у вигляді залежності тиску газу від концентрації молекул та температури:

р = nkТ. (3) Середня повна кінетична енергія молекули:

ε = і

kT,

де і – число ступенів свободи молекули.

Швидкості газових молекул:

середня квадратична

Vкв. =

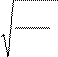3kT

m0

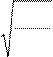8kT

3RT

= M;

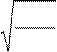8RT

середня арифметична

V = =

πm0

2kT

πM;

M

2RT

найбільш ймовірна

де m0 – маса однієї молекули.

Vім = =,

m

0

Основне рівняння молекулярно – кінетичної теорії ідеального газу записується ще й так:

< V

P = 1 nm

3 0

кв.

>2.

2.3. Перший закон термодинаміки

Важливою характеристикою термодинамічної системи є її внутрішня енергія U. Внутрішня енергія – це сума енергій хаотичного (теплового) руху мікрочастинок системи (молекул, атомів, електронів, ядер тощо) та енергії взаємодії цих частинок. Внутрішня енергія – однозначна функція термодинамічного стану системи.

Внутрішня енергія ідеального газу визначається за формулою:

U = m

M

де і – число ступенів свободи.

i

RT,

Перший закон термодинаміки є законом збереження і перетворення енергії стосовно до теплових процесів. В неізольованих термодинамічних системах цей закон формулюється як закон рівності між прибуттям і витратою енергії в системі.

Дата добавления: 2014-01-05