Специфіка філософського знання. 7 страница

∆).

Математична обробка результатів непрямих вимірювань

Розглянемо величину z, що є функцією декількох аргументів z = f(x,y,…), а величини х,у,... визначаються шляхом прямих вимі- рювань. Тоді послідовність розрахунків така.

1. Середнє значення z розраховують один раз, підставляючи за- мість аргументів х,у,... їх середні значення:

< z >=

f(< x >,<

y >,...). (9)

2. Визначають відносну похибку непрямих вимірювань εz за фо- рмулою:

ε = { д(lnf) ∆ +

z дx x

д(lnf) ∆

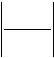дy y

+...}, (10)

де ∆х, ∆у – довірчі границі сумарних похибок вимірювань величин х,у,..... Для полегшення обчислень формулу (10) для розрахунку від- носної похибки непрямих вимірювань εz наводять у кожній лаборато- рній роботі.

3. Розраховують довірчу границю сумарних похибок:

∆ z = εz

< z >. (11)

4. Записують кінцевий результат у стандартній формі (3):

z =< z > ±∆ z, Pz, εz.

5. Роблять аналіз і висновки.

Примітка 1. Якщо в розрахунках використовують табличне зна- чення, то відповідну довірчу границю похибок визначають як полови- ну одиниці його (табличного значення) останнього значущого розряду з достовірністю, яка дорівнює одиниці.

Наприклад: g = 9,807 м/с2, ∆g = 0,0005 м/с2, Рg=1. Але, якщо g = 9,8 м/с2, ∆g = 0,05 м/с2, Рg =1.

Примітка 2. Якщо прямі вимірювання не можна виконати в од-

накових умовах, то величину z розраховують для кожного окремого вимірювання, а потім знаходять її середнє значення. При цьому для

прямих вимірювань беруть до уваги лише довірчу границю система-

тичних похибок, а відносні похибки прямих і непрямих вимірювань оцінюють тільки для якогось одного вимірювання.

Запитання для самоконтролю

1. Дайте визначення похибок: абсолютної похибки та відносної похибки вимірювання.

2. Що таке випадкове відхилення результату вимірювання і чим воно відрізняється від похибки вимірювання?

3. Чим відрізняється похибка вимірювання від довірчої границі похибок?

4. Як визначити довірчу границю систематичних, випадкових та сумарних похибок?

5. Як розрахувати значення величини, що вимірюється при не- прямому способі?

6. Розкрийте зміст поняття достовірності (довірчої ймовірності).

7. Якою є стандартна форма представлення кінцевого результату вимірювань?

ЛАБОРАТОРНІ РОБОТИ ПО МОДУЛЮ 1

РОЗДІЛ 1. МЕХАНІКА РОБОТА 1.1

ВИЗНАЧЕННЯ ПРИСКОРЕННЯ ВІЛЬНОГО ПАДІННЯ ЗА ДОПОМОГОЮ МАТЕМАТИЧНОГО МАЯТНИКА

Мета роботи: виміряти прискорення вільного падіння за пері- одом коливань математичного маятника; вивчити методику матема- тичної обробки результатів прямих і непрямих вимірювань; вивчити закони гармонічного коливального руху.

Прилади та обладнання: важка кулька, яка підвішена на лег-

кій нитці, що не розтягується; вертикальна шкала; секундомір.

Рух тіла під дією тільки однієї сили тяжіння називається вільним падінням, а прискорення, якого набуває при цьому тіло, − прискорен- ням вільного падіння g.

α

Q

α

F

mg

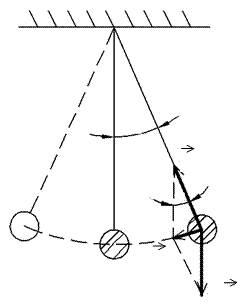
Pис.1

У даній роботі прискорення ві- льного падіння визначається за допо- могою математичного маятника.

Математичним маятником нази- ва-ється матеріальна точка, яка підві- шена на тонкій невагомій нитці, що не розтягується. Ця матеріальна точка здійснює коливання у вертикальній

площині під дією сили тяжіння.

На практиці математичним мая- тником можна вважати важке тіло, яке підвішене на легкій недеформованій нитці, довжина якої в багато разів бі- льша за розміри тіла.

На рис.1 видно, що сила F, яка пове- ртає маятник у напрямку до положен-

ня рівноваги, при малих кутах відхилення α дорівняє

F = mg sinα ≈ mgα, (1)

де sinα ≈ α

(у радіанах).

Таким чином, сила F пропорційна куту відхилення маятника від положення рівноваги, отже, пропорційна зміщенню маятника від цьо- го положення. Така сила викликає гармонічний коливальний рух.

Період коливань математичного маятника Т залежить від довжини маятника l і прискорення вільного падіння:

T = 2π

g

. (2)

Розв’язуючи (2) відносно g, одержимо:

g = 4π l. (3)

T

Звідки випливає, що визначення прискорення вільного падіння зво- диться до вимірювання довжини маятника та періоду його коли- вань.

Порядок виконання роботи

1. Установлюють певну (якомога більшу) довжину нитки маятника і знаходять значення l, вимірюючи для цього відстань від точки підвісу до центра ваги підвішеного тіла.

2. Відводячи маятник від положення рівноваги на малий кут (5−10o), визначають проміжок часу, за який здійснюється N = 50 повних коливань. Вимірювання повторюють не менше трьох ра-

зів.

3. Обробляють результати вимірювань l і t.

4. Розраховують середнє значення величини

N

〈T〉 = 〈t〉

〈T〉

за формулою

і середнє значення величини

〈g〉

за формулою (3).

5. Визначають відносні похибки результатів прямих і непрямих

вимірювань:

ε T = ε t;

ε g = 2ε π

+ εl + 2ε.

6. Розраховують довірчу границю сумарних похибок

T

∆ g =〈g〉ε g.

7. Оформлюють звіт і результати заносять у таблицю.

№   п/п	Табличні величини	Результати прямих вимірювань	Результати непрямих вимірювань
π	l, м	t, с	T, с	g, м/с2
с	−			−	−

Запитання для самоконтролю

1. Сформулюйте закон всесвітнього тяжіння.

2. Поясніть різницю між вагою і силою тяжіння.

3. Запишіть залежність прискорення вільного падіння від висо- ти над поверхнею Землі та географічної широти місця.

4. У чому полягає різниця між фізичним і математичним маят- никами? Порівняйте вирази для їх періодів коливань.

5. Запишіть диференціальне рівняння гармонічних коливань і його розв'язок. Поясніть зміст понять "зміщення", "амплітуда", "поча- ткова і повна фази", "період", "частота коливань".

6. Від яких величин залежить повна енергія гармонічних коли-

вань?

РОБОТА 1.2

ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ ТІЛА МЕТОДОМ КРУТИЛЬНИХ КОЛИВАНЬ

Мета роботи: вивчити динаміку обертального руху твердого тіла; визначити момент інерції тіла методом крутильних коливань.

Прилади та обладнання: крутильний маятник, циліндр, секун- домір, штангенциркуль.

У даній роботі для визначення моменту інерції тіла неправиль- ної форми використовують крутильний маятник, який являє собою підвішений на пружному дроті диск зі скобою (рис.1).

 

Період коливань маятника T зв'язаний з його моментом інерції співвідношенням:

Т = 2π J

k

, (1)

Pис.1

де k − модуль кручення підвісу, який чисель- но дорівнює моменту сили, що закручує дріт на кут в один радіан.

Для виключення k з виразу (1) діють так. На диску розміщують циліндр з відомим момен-

том інерції Jц У цьому випадку згідно з (1) пе- ріод маятника дорівнюватиме

T1 = 2π

J + Jц

k

. (2)

Розв'язуючи сумісно (1) і (2)одержують:

J = J

T

цT2 −T2

, (3)

де J

= 1 mr2 = 1 md2, (4)

ц 2 8

де m, d − маса і діаметр циліндра.

Порядок виконання роботи

1.Записують задане значення маси циліндра m.

2. Вимірюють штангенциркулем діаметр циліндра d (не менше трьох разів).

3. Крутильний маятник приводять у коливальний рух, поверну-

вши його на невеликий кут (20-30°). Вимірюють час t тридцяти коли- вань (N=30). Вимірювання повторюють п'ять разів.

4. На диск ставлять циліндр і, повторюючи вимірювання (див.

п.3), визначають час t1.

5. Розраховують середні значення ‹ t ›, ‹ t1›, ‹ d ›.

6. Обчислюють середнє значення періодів коливань

〈T 〉 =

〈t〉

〈T 〉 =

〈t1 〉

N і N

, а також середні значення моментів іне-

рції ‹ Jц › і ‹ J › за формулами (4) і (З).

7. Визначають відносні похибки і довірчі границі сумарних по-

хибок результатів вимірювань, використовуючи формули:

ε

J

ε =

ц m

+ 2ε d;

εT

ε T = ε t;

t

=;

ε

1 1

ε =ε

+

+ 2ε

2∆T 〈T1〉 + 2∆T 〈T 〉.

J J T

ц

〈T1〉 −〈T 〉

8. Оформлюють звіт і висновки, заносячи дані в таблицю.

№ п/п	Задані величи- ни	Результати прямих вимірювань	Результати непрямих вимірювань
m, кг	d, м	t, с	t1, с	N	T, с	T1, с	Jц, кг м2	J, кг м2
c	−					−	−	−	−

Запитання для самоконтролю

1. Дайте визначення моменту інерції матеріальної точки і тіла довільної форми.

2. Запишіть і сформулюйте теорему Штейнера, проілюструйте рисунком.

3. Наведіть відомі Вам моменти інерції тіл симетричної форми.

4. Виведіть формулу кінетичної енергії тіла, що обертається.

5. Дайте визначення моменту імпульсу твердого тіла, що обер- тається відносно осі обертання.

6. Запишіть і сформулюйте основний закон динаміки обертального

руху.

РОБОТА 1.3

ВИЗНАЧЕННЯ МОДУЛЯ ЮНГА ПО ЗГИНУ СТЕРЖНЯ

Мета роботи: визначити модуль пружності (модуль Юнга) для сталі.

Прилади та обладнання: прилад для визначення модуля Юнга по стрілі прогину, лінійка, штангенциркуль, набір тягарців, індикатор.

Зміну в розміщенні частинок твердого тіла під дією зовнішніх сил називають деформацією. Зміну довжини ∆l при односторонньому розтягу (або стиску) називають абсолютною деформацією, а відно-

∆l

шення l

− відносною деформацією, де l − початкова довжина.

Деформація викликає виникнення в деформованому тілі пружної сили Fпр:

F

пр.

= −k∆l, (1)

де k - коефіцієнт жорсткості, який залежить від матеріалу і форми ті- ла. Формула (1), що виражає закон Гука, дійсна для пружних дефор- мацій. Сила F, яка діє на площу поперечного перерізу тіла S, створює нормальну напругу

Відповідно до закону Гука

F

σ = S. (2)

σ = E ∆l, (3)

l

де E - модуль Юнга, постійний для даної речовини коефіцієнт, який характеризує її пружні властивості.

З формули (3) випливає, що модуль Юнга чисельно дорівнює на-

прузі, при якій відносна деформація дорівнює одиниці (тобто

∆l = l).

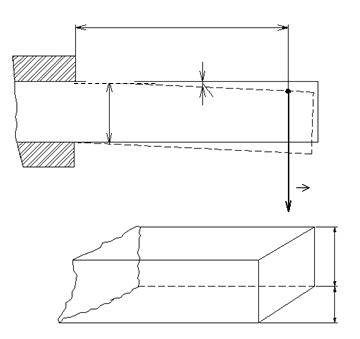
Модуль Юнга можна визначити по згину стержня прямокутного

перерізу (рис.1) за формулою

E = l ⋅ F

ab3 λ

, (4)

де l − відстань від точки опори стержня А до точки В прикладення сили F; a і b − ширина і товщина стержня в прямокутній частині; λ − стріла прогину (тобто та відстань, на яку опускається при деформації точка С, яка лежить посередині між А і В). Стріла прогину залежить від величини навантаження, розмірів і форми стержня, а також від мо- дуля Юнга матеріалу стержня.

  А

ℓ

А

А C B

b λ

F

b

a

Pис.1

Порядок виконання роботи

І. Вимірюють лінійкою довжину стержня l від опори А до точки В прикладення деформуючої сили (тобто до ребра призми, на якій підвішен тягар).

2. Вимірюють штангенциркулем ширину a і товщину b стержня у вузькій прямокутній його частині.

3. У середньому положенні С закріплюють стрілочний індика- тор так, щоб рухомий щуп був засунутий у корпус індикатора. При

утворенні стріли прогину щуп повинен виходити з корпусу індикато-

ра.

4. Поворотом зовнішнього кільця з насічкою на боковій поверх- ні встановлюють шкалу індикатора в нульове положення.

5. Чашку підвісу послідовно навантажують плоскими важками

масою від 1 до 5 кг, а потім розвантажують до 0 кг. Для кожного на-

вантаження

F = mg

за шкалою індикатора визначають два положен-

ня стріли прогину λ (при навантаженні і розвантаженні).

6. Будують графіки залежності F від λ при навантаженні і розвантаженні (вони практично зливаються в одну пряму лінію, що проходить через початок координат, оскільки при вказаних навантаженнях деформація згину є пружною).

7. Користуючись графіком, визначають величину

F

〈 λ 〉

як від-

ношення ординати правого кінця графіка до відповідної абсциси (таке відношення називають кутовим коефіцієнтом).

8. Розраховують середнє значення модуля Юнга за формулою

(4) і відносну похибку вимірювань за формулою:

ε E = 3ε l + ε a + 3ε b + ε λ + ε F.

E

9. Визначають довірчу границю ∆ E

при Р ≥ 0,95.

= ε 〈E〉

сумарних похибок

10. Оформлюють звіт і висновки, вносячи дані в таблицю.

№ п/п	Результати прямих вимірювань	Результати непрямих вимірювань
l, м	a, м	b, м	F, H λ м	E, Па
c				−	−

Запитання для самоконтролю

1. Дайте визначення абсолютної і відносної, пружної і непруж- ної та залишкової деформації.

2. Перелічіть відомі види деформації.

3. Запишіть і сформулюйте закон Гука (в загальному вигляді і для одностороннього розтягу або стиску).

4. Розкрийте фізичний зміст модуля Юнга.

5. Нарисуйте діаграму розтягу і вкажіть точки, що відповідають границям пружності і міцності. Вкажіть границі виконання закону Гу- ка і границі пластичних деформацій.

6. Поясніть відмінності в пружних властивостях пластичних і

крихких, а також аморфних і кристалічних тіл.

РОЗДІЛ 2. МОЛЕКУЛЯРНА ФІЗИКА ТА ТЕРМОДИНАМІКА РОБОТА 2.1

ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ВНУТРІШНЬОГО ТЕРТЯ РІДИНИ МЕТОДОМ СТОКСА

Мета роботи:: вивчити механізм явища переносу – внутрішнє тертя; визначити коефіцієнт внутрішнього тертя рідини за швидкістю рівномірного падіння кульки.

Прилади тa обладнання: скляний циліндр, наповнений ріди- ною; металеві кульки, мікрометр, секундомір.

При протіканні шарів рідини (або газу) з різними швидкостями між ними виникає тертя. Завдяки тепловому руху молекули перехо- дять з одного шару в інший і при цьому кожна молекула переносить разом із собою імпульс свого направленого руху (mv). У результаті з двох суміжних шарів більш швидкий шар збагачується "повільними" молекулами, а більш повільний − "швидкими". Через це з боку шару, що рухається швидше, на шар, що рухається повільніше, діє приско- рююча сила, і навпаки, з боку шару, що рухається повільніше, на більш швидкий шар діє гальмуюча сила. Ці сили називають силами внутрішнього тертя, або силами в’язкості. Вони направлені по дотич- ній до поверхні шарів (рис 1).

Згідно із законом Ньютона сила внутрішнього тертя F, що діє в площині дотикання двох паралельних суміжних шарів рідини (або га-

∆v

зу), пропорційна площі їх дотикання S і градієнту швидкості

∆z:

∆v

F = mη ∆z S

, (1)

де ∆v = v2 ─ v1, v1 і v2 − швидкості шарів; ∆z

− відстань між ша-

рами; знаки m у формулі (1) відповідають гальмуючій і прискорюю- чій силам. Коефіцієнт пропорційності η називається коефіцієнтом внутрішнього тертя, або коефіцієнтом в’язкості. Він чисельно дорів- нює силі внутрішнього тертя, яка діє на одиницю площі дотикання шарів при градієнту швидкості, що дорівнює одиниці.

Завдяки в'язкості тіло, що рухається в рідині, захоплює прилеглі

до нього. шари і тому зазнає опору з боку рідини. Згідно із законом Стокса при невеликій швидкості руху тіла сила опору F пропорційна коефіцієнту в'язкості η, швидкості тіла v та його лінійним розмірам l

: F ~ ηvl.

Для кульки з радіусом r

F

= 6πηvr. (2)

На кульку масою m і радіусом r, що рухається в рідині зі швидкістю V, діють три сили: сила опору F, сила тяжіння P та Архімедовa сила FA. Останні дві сили визначаються за формулами:

4

Р = mg = 3 πr

gρ1; (3)

F A =

4 3

3 πr

g ρ 2

, (4)

де g − прискорення вільного падіння, ρ1 − густина кульки, ρ 2 − гус- тина рідини.

При вертикальному падінні кульки в рідині сила опору, як і aрхімедовa сила, направлена вгору (рис.2). Оскільки P і FA сталі, а сила F зростає зі збільшенням швидкості, то настане такий момент, коли буде досягнуто рівності P=FA+F. Починаючи з цього моменту, рух кульки буде рівномірним. Підставляючи в останню рівність вира- зи (2) – (4), маємо:

4 3

3πr

4 3

gρ1 = 3 πr

gρ 2 + 6πηrv.

z V2

∆z -F S

F

V1 х

F

a

ℓ FA

Р

b

Pис.1 Pис.2

Звідси знаходимо:

= 2 ρ1 − ρ2 2,

або

η 9 v gr

η = 1

18

⋅ gd l

t (ρ1 − ρ2).

(5)

де d =2r, a l = vt − шлях, який пройшла кулька за час t.

Порядок виконання роботи

1. Вимірюють відстань l між мітками "a" і "b" циліндричної по- судини, що наповнена рідиною (гліцерин).

2. Мікрометром вимірюють діаметр d трьох кульок (приблизно однакових).

3. Кидають кульку в рідину так, щоб вона рухалася вздовж

центральної частини циліндра; вимірюють час падіння t між мітками

"a" і "b".

4. Експериментальні дані d, l, t і табличні ρ1 і ρ 2 заносять у таблицю.

5. Розраховують значення η за формулою (5) для кожного вимі- рювання, а потім знаходять (η).

6. Визначають відносні похибки і довірчі границі для одного з

вимірювань за формулами:

ε

+

η = ε t

+ ε l

+ 2ε d

+ ε g

ε ρ1−ρ 2;

∆ +

= ρ1

∆ ρ2

−; ∆

= 〈η 〉ε.

ε ρ1 ρ2

ρ1 − ρ 2 η η

№ п/п	Табличні дані	Результати прямих вимірювань	Результати непрямих вимірювань
ρ1, кг/м3	ρ 2,кг/м	g,м/с	l, м	d, м	t, с	η, Па с
с	−	−	−				−

Запитання для самоконтролю

1. Поясніть механізм виникнення сил внутрішнього тертя.

2. Сформулюйте і запишіть закон внутрішнього тертя (закон

Ньютона), дайте ілюструючий рисунок.

3. Що називається градієнтом швидкості? Який йoгo зміст?

4. Що називається коефіцієнтом внутрішнього тертя? В яких одиницях він вимірюється? Який його фізичний зміст?

5. При яких умовах кулька рухається в рідині рівномірно?

6. Сформулюйте і запишіть закон Стокса.

РОБОТА 2.2

ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ПУАССОНА ГАЗУ МЕТОДОМ АДІАБАТИЧНОГО РОЗШИРЕННЯ (МЕТОД КЛЕМАНА- ДЕЗОРМА)

Мета роботи: визначити коефіцієнт Пуассона повітря і порівня- ти результат експерименту з висновками молекулярно-кінетичної тео- рії газів.

Прилади та обладнання: закритий скляний балон з краном, ма- нометр, насос.

Молярною теплоємністю С будь-якої речовини називають фізич- ну величину, що чисельно дорівнює кількості теплоти, яку треба нада-

ти одному молю цієї речовини для підвищення його температури на

один кельвін.

Теплоємність газу суттєво залежить від умов, при яких надають теплоту. Так, якщо нагрівається газ при сталому об'ємі, то кількість теплоти витрачається на збільшення його внутрішньої енергії. Якщо ж

газ нагрівати при сталому тиску, то він потребує ще додаткової кіль-

кості теплоти для виконання роботи при розширенні. Тому молярна теплоємність CP при сталому тиску більше молярної теплоємності при сталому об'ємі CV. Зв'язок між ними показує співвідношення Майєра:

Дата добавления: 2014-01-05