Движение деформируемой жидкой частицы

Качанов И.В,

Ч а с т ь 2

Минск

БНТУ

УДК 532.5 – 533.6

ББК 30.123я7

К 30

Рецензенты:

доктор технических наук, профессор В.И. Байков,

доктор физико-математических наук В.А. Бабенко

К 30Механика жидкости и газа: курс лекций: в 4 ч. / И.В.Качанов,

В.В.Кулебякин, В.К.Недбальский. – Минск: БНТУ, 2011. – Ч.2.-

Издание содержит изложение основных разделов механики жидкости и газа в объеме курса лекций, предусмотренных учебным планом для строительных специальностей БНТУ. Может быть использовано в самостоятельной работе студентов, для подготовки к экзаменам и зачетам, при проведении лабораторных работ и практических занятий, окажет большую помощь студентам других специальностей, изучающих гидравлику.

Движение жидкой частицы является более сложным, чем в случае твердого тела, которое, как известно из механики, может складываться из поступательного движения полюса и вращательного движения тела относительно этого полюса. Особенностью частиц жидкости, как уже неоднократно отмечалось, является текучесть, т.е. легкая деформируемость их под действием самых ничтожных сил. Поэтому, помимо поступательного и вращательного, жидкая частица может участвовать также в деформационном движении. Это положение и составляет суть так называемой первой теоремы Гельмгольца, к рассмотрению которой мы приступаем. Важнейшим достоинством приводимых ниже выкладок и рассуждений, достаточно простых, но требующих внимания, является то, что они раскрывают физический смысл и вносят ясность в ряд казалось бы совершенно абстрактных понятий.

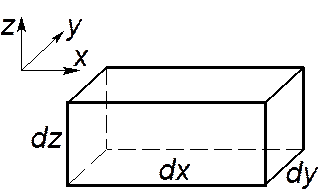
Рассмотрим жидкую частицу в форме прямоугольного параллелепипеда. Длина его ребер dx, dy, dz. Деформация такой жидкой частицы может быть как линейной (ребра удлиняются и укорачиваются), так и угловой (возникает перекос граней). Удобным представляется рассмотрение каждого из этих видов деформаций раздельно.

Угловые деформации.

Из вышеприведенного рисунка следует, что угловая деформация (перекос граней и углов между ними) может возникнуть из-за разности скоростей, перпендикулярных ребрам. Для упрощения ограничим рассмотрение лишь одной гранью, показанной на следующем рисунке.

Пусть компоненты скорости в точке A равны 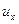, , 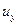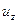. Найдем скорости в точке B, считая, что движение установившееся и, следовательно, все производные по времени равны нулю. Приращение компоненты скорости при переходе из одной точки пространства в другую можно представить как u+du. Так для проекции 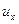можем записать 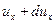, где, очевидно, что

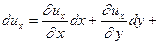
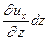(1.1)

Аналогичные выражения можно записать и для других проекций.

Рассмотрим приращение 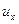при переходе от точки A к точке B. В этом случае 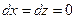, т.е.

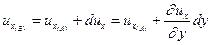
Предположим, что за время dt из-за разности скоростей в точках A и B ребро займет положение AB'.

Аналогично рассуждая относительно компоненты скорости 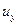в точках A и D, получим:

Точка A: 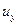(по условию)

Точка D: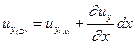

В связи с разностью этих скоростей точка D займет позицию D'. Таким образом, получим:

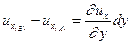
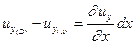
Путь, который проходит точка B за время dt, попадая в положение B', определяет величину перекоса, которую можно найти как

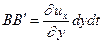
Угловая деформация характеризуется тангенсом угла 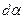. При этом

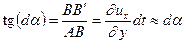
(имея в виду, что ).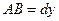

Вследствие малости угла 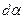можно считать, что .

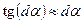Аналогично рассуждая, можно получить, что:

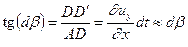
Полный перекос первоначально прямого угла A определится соответственно, как сумма:

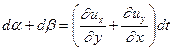(1.2)

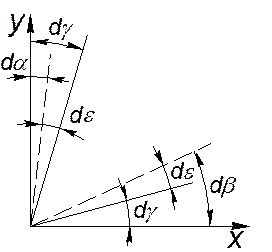
Здесь следует обратить внимание на одно весьма существенное обстоятельство, а именно: рассматриваемое перемещение ребер вызвано не только деформацией, но и вращением частицы. Действительно, если бы грань только деформировалась без вращения, то ребра повернулись бы на одинаковый угол навстречу друг другу. Наоборот, в случае, если бы происходило только вращение, то ребра поворачивались бы на одинаковый угол в направлении вращения. Таким образом, в общем случае движение жидкого элемента можно рассматривать как сумму деформационного и вращательного движений, характеризуемых соответствующей комбинацией 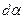и . 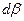Рассмотрим деформацию прямого угла A, считая, что вращение происходит против часовой стрелки. Чисто деформационное движение будем характеризовать углами 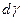, а чисто вращательное - .

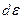Из рисунка следует, что

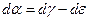и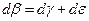

т.е ,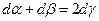

откуда

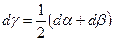(1.3)

Вычитая, получим

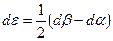(1.4)

Таким образом, приходим к выводу, что деформация характеризуется полусуммой углов, а вращение – их полуразностью. В соответствии с соотношением (1.2), можно записать:

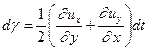(1.5)

Таким образом, получим скорость угловой деформации, происходящей вокруг оси z

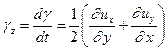(1.6)

И по аналогии относительно других осей:

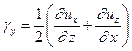(1.7)

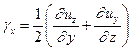(1.8)

По определению 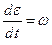есть угловая скорость вращения жидкой частицы. Проекции угловых скоростей при этом определятся из формул:

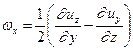(1.9)

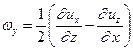(1.10)

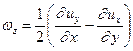(1.11)

Вышеприведенные соотношения играют исключительно важную роль в механике жидкости и газа. Они устанавливают связь между угловой и поступательной скоростями деформируемой жидкой частицы. Вопрос о знаках – это вопрос выбора. В гидромеханике обычно поворот против часовой стрелки считается положительным, по часовой - отрицательным.

В векторной форме выражение для угловой скорости может быть записано как:

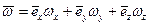(1.12)

Заменяя 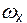, 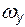и 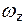их выражениями из (1.9-1.11) получаем:

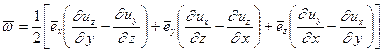(1.13)

Учитывая соотношения векторной алгебры (применительно к вектору скорости жидкой частицы), можем записать:

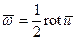(1.14)

либо

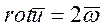(1.15)

Формула (1.15) раскрывает гидромеханический смысл вихря (ротора) векторного поля скоростей. Если 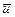характеризует поле мгновенных скоростей, то векторное поле 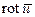представляет собой поле удвоенных угловых скоростей частиц жидкости этого поля.

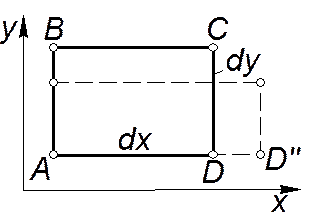
Линейные деформации.

Очевидно, что линейные деформации жидкой частицы могут возникнуть в результате различия в скоростей в точках, совпадающих с направлением ее ребер. Полагаем, как и ранее, компоненты скорости в точке A равными: , , .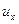

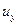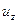Вдоль оси x:

Точка A: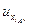

Точка D: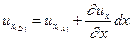

Разность скоростей, вызываю­щая удлинение ребра AD: 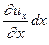. Удлинение частицы 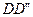за время dt

(1.16)

Относительное удлинение

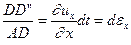(1.16)

Скорость относительного удлинения

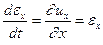(1.17)

Аналогичные выражения можно получить для других осей:

;

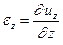
Если процесс происходит одновременно вдоль всех осей, то это приводит к объемному расширению либо сжатию частицы. Таким образом, объемная деформация сводится к изменению первоначального объема параллелепипеда 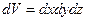на величину 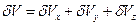за счет растяжения либо сжатия ребер. При этом 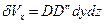, и с учетом (1.16) 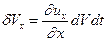. К аналогичным выводам можно для изменений по другим осям координат 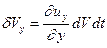и 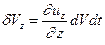. Таким образом:

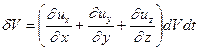
Скоростью относительной объемной деформации назовем отношение изменения объема к его первоначальному объему и скорости деформации, т.е.

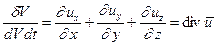
Если 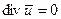, то это означает, что 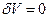, т.е. деформация жидкой частицы происходит без изменения её объема. В этом и заключается гидромеханический смысл равенства нулю дивергенции вектора скорости.

Полученную выше связь между поступательной и вращательной скоростями жидкой частицы можно получить и более коротким путем, представляющим определенный интерес. Разные подходы к одному и тому же вопросу способствуют углубленному пониманию. Поэтому рассмотрим также этот путь.

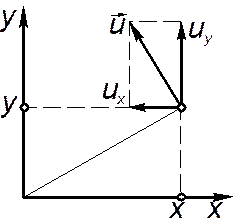
Пусть жидкая частица вращается вокруг оси z с угловой скоростью 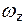. Запишем выражение для ротора скорости в проекциях на оси координат. Имеем:

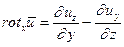
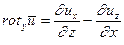
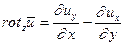
Рассмотрим точку M на жидкой частице.

Линейная скорость этой частицы 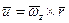. Запишем выражения для проекций скоростей на оси координат:

;

;

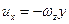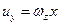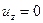
Откуда находим ; .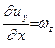

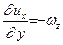Таким образом:

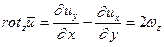
Аналогично для двух других компонент

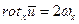; и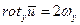

Либо в векторной форме

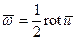
что полностью совпадает с (1.14).

Движение, при котором 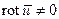называют вихревым, если же 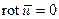- безвихревым, либо потенциальным. Высказанное означает, что если течение вихревое, то движение жидких частиц происходит с вращением.

Дата добавления: 2014-01-05