Преобразования Громеки-Лэмба

Рассмотрение теоремы Гельмгольца о движении жидкой частицы показывает, что жидкость, как любое материальное тело, может участвовать в поступательном и вращательном движениях, но, кроме того – в деформационном. Следует учесть, что для совершения работы в современных технических устройствах может быть использована лишь энергия поступательного движения. Энергия же вращательного (вихревого) движения полностью теряется, рассеивается в окружающей среде, превращаясь в тепло. Как говорят, происходит диссипация механической энергии в тепловую.

Система уравнений Эйлера для движения идеальной жидкости в явной форме не учитывает факт существования вращательного движения. Поэтому для получения уравнений, учитывающих эту особенность движения жидких частиц целесообразно использовать преобразование, называемое преобразованием Громеки-Лэмба. Формально оно сводится к тому, что в выражении для ускорения выделяются члены, характеризующие вращение жидких частиц.

Рассмотрим лишь одну компоненту ускорения (в проекции на ось х):

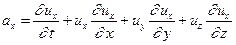(4.1)

Прибавим и вычтем в конвективной части ускорения выражение

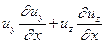
Скомпонуем члены получившегося выражения с учетом их знаков:

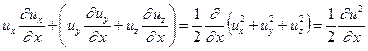
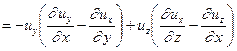
Выражения в скобках, очевидно, есть не что иное, как удвоенные компоненты вихря 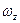и 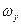, т.е. можно записать:

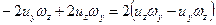
Подставляя полученные значения в (4.1) имеем

(4.2)

и по аналогии

(4.3)

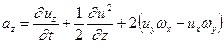(4.4)

В векторной форме выражение для ускорения будет иметь вид:

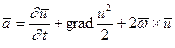(4.5)

Если движение установившееся, то

(4.6)

Уравнения движения в форме Громеки-Лэмба.

Если в правую часть уравнений Эйлера подставить ускорение в виде (4.5) либо (4.6), то это приводит к уравнению движения в форме Громеки-Лэмба. Для установившегося движения имеем

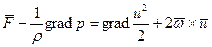(4.7)

Выполним некоторые преобразования (4.7).

В разделе гидростатики было введено понятие о скалярной функции, называемой силовой. Было показано, что

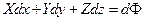(4.8)

Поскольку эта функция является полным дифференциалом, то можно записать

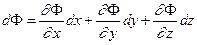(4.9)

Сопоставляя (4.8) и (4.9), получаем

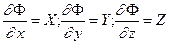(4.10)

С другой стороны вектор 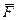, проекциями которого являются X, Y, и Z

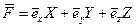(4.11)

Из (4.10) и (4.11) следует, что

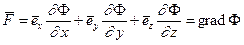(4.12)

С учетом (4.12) выражение (4.7) принимает вид

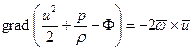(4.13)

Следует иметь в виду, что эта форма записи справедлива лишь для несжимаемой жидкости, т.е. при условии 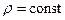. И, наконец, уравнению движения (4.13) можно придать более удобную для анализа форму, умножив скалярно его левую и правую части на произвольный направленный отрезок

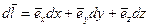(4.14)

Опуская подробное изложение этой операции, приведем лишь конечный результат:

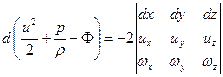(4.15)

Интегрирование уравнения движения для установившегося течения

Интегрирование уравнения движения (4.15) возможно лишь в случае, когда его правая часть равна нулю. Из теории определителей известно, что признаками равенства нулю являются: равенство нулю какой-либо строки или пропорциональность элементов одной строки элементам другой.

Исходя из физического смысла величин, составляющих определитель, имеем четыре возможных случая:

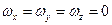(4.16)

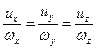(4.17)

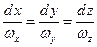(4.18)

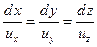(4.19)

Для любого из них можем записать

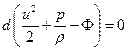
И после интегрирования:

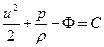(4.20)

Если из массовых сил действует только сила тяжести, то, как показано при рассмотрении гидростатики,

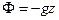
и (4.20) принимает вид

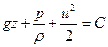(4.21)

Еще раз обратим внимание на то, что вид уравнения (4.21) одинаков вне зависимости от того, какой из четырех случаев равенства нулю определителя рассматривается. Однако смысл интеграла и область его применения различны. Именно поэтому следует разобраться в этом вопросе подробней.

Первый случай, как известно, является признаком потенциальности движения. Интеграл (4.21) в этом случае называют интегралом Коши-Лагранжа. Он справедлив для любых точек жидкости, движущейся без вращения частиц, т.е. потенциально.

Второй случай является признаком коллинеарности вектора вихря и вектора скорости. Это весьма редкий случай так называемого винтового движения.

Третий случай характеризует движение жидкой частицы вдоль вихревой линии, а четвертый - движение вдоль линии тока. Интеграл (4.21) при этом носит название интеграла Бернулли. Он справедлив как для потенциального, так и для вихревого движений, но только вдоль линии тока (не во всем объеме жидкости).

Дата добавления: 2014-01-05