Модель вязкой жидкости

Приступая к рассмотрению движения вязкой жидкости, необходимо прежде всего уяснить терминологию, т. е. смысл, вкладываемый в понятие «вязкая жидкость». С математических позиций необходимо установить вид функциональной зависимости для напряжений, т.е., другими словами, сформулировать модель вязкой жидкости. В дальнейшем под вязкой мы будем понимать жидкость, удовлетворяющую трем гипотезам: линейности, однородности и изотропности

Гипотеза линейности.

Применим закон Ньютона для вязкости к жидкости, движущейся параллельно плоскости xOy (см. рисунок), что дает:

Воспользуемся результатом, полученным при рассмотрении теоремы Гельмгольца о движении жидкой частицы. Согласно выводам, полученным при ее рассмотрении, скорость угловой деформации относительно оси y

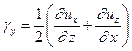
Учитывая, что рассматривается движение в плоскости xOy, и, следовательно, :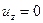

И, значит, касательное напряжение можно определить, как:

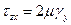(5.1)

Полученный результат иллюстрирует так называемый закон трения Стокса. Согласно этому закону, напряжения, возникающие в жидкости, в отличие от твердого тела, пропорциональны не величинам самих деформаций, а скоростям деформаций, и связаны с ними линейной зависимостью. При этом коэффициент пропорциональности остается неизменным и равным 2.

Кроме того, согласно закону Стокса касательные напряжения, как показано выше, пропорциональны скоростям угловой деформации, а нормальные - скоростям линейной деформации, т.е. , , .

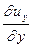Таким образом, можем записать:

(5.2)

и т.д. (для компонент по другим осям координат).

Рассмотрим теперь нормальные напряжения, возникающие из-за сил вязкости. Согласно закону Стокса, их можно записать в виде так называемых девиаторов напряжения, имеющих вид:

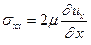
(5.3)

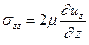
Полные нормальные напряжения отличаются тем, что помимо записанных выше компонент, обусловленных вязкостью, в любой, как в вязкой, так и в невязкой жидкости, действует гидростатическое давление. Таким образом, полные нормальные напряжения следует записать как сумму (с учетом знака):

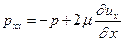
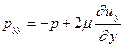(5.4)

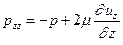
Выполним следующую операцию: из утроенной величины вычтем сумму ().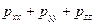

Получим:

откуда найдем:

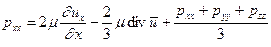
В качестве давления в вязкой жидкости принимают среднее арифметическое, т.е.

.

И, следовательно,

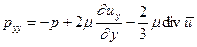(5.5)

Для несжимаемой жидкости 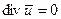, и выражения соответственно упрощаются.

Гипотеза однородности

Предполагается, что вид линейной зависимости между напряжениями и скоростями деформаций одинаков для всех точек пространства.

Гипотеза изотропности

Вязкая жидкость предполагается изотропной, т.е. ее свойства в любом направлении одинаковы.

Дата добавления: 2014-01-05