Одномерная модель течения вязкой несжимаемой жидкости

Качанов И.В,

Ч а с т ь 3

Модель вязкой жидкости

Преобразования Громеки-Лэмба.

Потенциальное движение жидкости

6. Уравнения движения вязкой жидкости (уравнения Навье-Стокса

Минск

БНТУ

УДК 532.5 – 533.6

ББК 30.123я7

К 30

Рецензенты:

доктор физико-математических наук С.П.Фисенко

доктор физико-математических наук В.А. Бабенко

К 30Механика жидкости и газа: курс лекций: в 4 ч. / И.В.Качанов,

В.В.Кулебякин, В.К.Недбальский. – Минск: БНТУ, 2011. – Ч.3.-

Издание содержит изложение основных разделов механики жидкости и газа в объеме курса лекций, предусмотренных учебным планом для строительных специальностей БНТУ. Может быть использовано в самостоятельной работе студентов, для подготовки к экзаменам и зачетам, при проведении лабораторных работ и практических занятий, окажет большую помощь студентам других специальностей, изучающих гидравлику.

Одномерными называются потоки, в которых основные параметры течения (скорости, давление и др.) зависят лишь от одной геометрической координаты, направление которой совпадает с направлением вектора скорости. Примером такого течения является рассматривавшееся ранее движение жидкости в элементарной трубке тока, ввиду малости поперечного сечения которой скорость и давление в нем постоянны. Использование модели одномерных течений позволяет достаточно просто решать многие важные практические задачи, а раздел прикладной гидромеханики, применяющий эту модель течения, называют гидравликой. Для решения широкого круга инженерных задач плодотворной оказалась так называемая струйная модель потока. Согласно этой модели поток представляется состоящим из бесконечного множества элементарных жидких струек. При рассмотрении потока поперечные сечения в нем выбираются так, чтобы пересекающие их линии тока в каждой точке сечения были направлены по нормали. В этом случае сечение потока называется живым. Вообще говоря, живое сечение представляет собой изогнутую поверхность, но, если линии тока в элементарных жидких струйках, составляющих его, параллельны, то живое сечение будет плоским.

Ранее было показано, что объемный расход элементарной струйки жидкости может быть определен как:

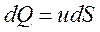
где u –скорость (постоянная) в поперечном сечении элементарной жидкой струйки,

dS - площадь ее сечения.

В соответствии со струйной моделью расход потока можно определить как: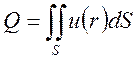

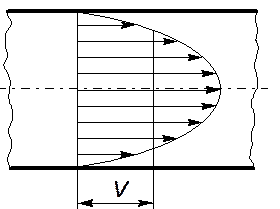
Рассмотрим движение вязкой жидкости в трубе круглого поперечного сечения. Для реального течения вязкой жидкости распределение скоростей в поперечном сечении трубопровода (эпюра скоростей) будет неравномерным, в частности, может иметь вид, показанный на рисунке.

Соответственно, запись 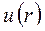в предыдущей формуле означает, что местные скорости в сечении трубы изменяются по радиусу, а 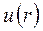представляет закон изменения скорости, т.е. является математическим описанием эпюры скоростей. Следовательно, для того, чтобы вычислить расход по этой зависимости, необходимо знать уравнение эпюры скоростей, которое, вообще говоря, априори неизвестно. С чисто математических позиций интеграл в правой части выражает объем эпюры скорости. Представим теперь, что при неизменном расходе Q жидкость становится идеальной, т.е. теряет вязкость. Это, очевидно, приведет к к перестройке эпюры скоростей, причем, поскольку исчезнут силы вязкого трения, все частицы жидкости будут двигаться с некоторой одинаковой скоростью V. При этом, ввиду того, что расход остается неизменным, объем новой эпюры скоростей равен объему старой. Таким образом, реализуется условие: 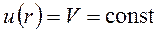и, соответственно, получаем:

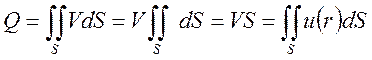
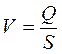
Скорость V, введенная таким образом носит название среднерасходной, либо средней скорости. Следовательно, формально средняя скорость может быть определена как фиктивная скорость, с которой должны были бы двигаться все частицы жидкости для того, чтобы расход был равен его истинному значению. Заменив истинные, неравномерно распределенные по сечению скорости средней скоростью V и приняв давление постоянным по живому сечению, мы заменяем рассмотрение реального потока течением, в котором все частицы жидкости имеют одну и ту же скорость. С физико-математической точки зрения использование понятия средней скорости позволяет свести задачу о движении жидкости в трубах и каналах к одномерной. Для такого течения решением упрощенной одномерной задачи является получение зависимости распределения давления по длине трубы, удобной для технических расчетов.

Если поперечное сечение трубы или канала изменяется по длине, то поток является трехмерным, но в некоторых случаях приближенно может быть сведен к одномерной модели. Это возможно, если кривизна линий тока и углы их расхождения малы. Потоки, удовлетворяющие этим условиям, называют плавно изменяющимися (параллельно струйными), живые сечения их слабо искривлены и могут считаться плоскими. Выбирая продольную координату вдоль оси потока, проходящей через центры инерции живых сечений, можно рассматривать плавно изменяющийся поток, как одномерный.

Рассмотрим свойства плавно изменяющегося движения несжимаемой жидкости в трубах и каналах с точки зрения перехода к одномерной модели. Если считать поток установившимся, то все производные по времени, входящие в уравнения движения, равны нулю. Если исходить из одномерной модели, то малы и могут быть приняты равными нулю также поперечные компоненты скорост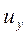и и 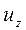. Применительно к этому случаю система дифференциальных уравнений Навье-Стокса принимает вид:

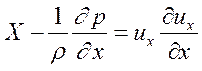
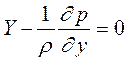
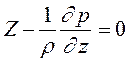
Последние два уравнения полностью совпадают с уравнениями гидростатики, а это означает, что в пределах живого сечения движущейся жидкости давление распределено по гидростатическому закону. В частности, если объемной силой является сила тяжести, то для произвольной точки, находящейся в живом сечении, имеем Y=0, Z= - g cos α, где α – угол между направлением вертикали и нормалью к вектору скорости. Следовательно, в пределах живого сечения (для Х= const) гидростатический напор постоянен:

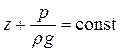(либо )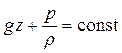

Этот вывод приближенно справедлив для плавно изменяющихся течений и позволяет распространить уравнение Бернулли на поток конечных размеров, введя в него средние по сечению величины.

Дата добавления: 2014-01-05