Лекция № 11

Способы задания отношений

Понятие отношения на множестве

Лекция № 10

В математике изучают не только связи между элементами двух множеств, т.е. соответствия, но и связи между элементами одного множества. Называют их отношениями.

Отношения многообразны. Между понятиями – это отношения рода и вида, части и целого, между предложениями – отношения следования и равносильности, между числами – «больше», «меньше», «равно» и т.д.

Если рассматриваются отношения между двумя элементами, то их называют бинарными, отношения между тремя элементами – тернарными, отношения между п элементами – п- арными. Примером тернарного отношения может служить отношение между точками прямой – «точка х лежит между точками у и z».

Примеры бинарных отношений встречаются не только в математике, но и всюду в жизни, вокруг нас: родственные и другие отношения между людьми (быть отцом, сестрой и т.д.), отношения между событиями во времени (раньше, позже, одновременно), между предметами по их расположению в пространстве (выше, ниже, левее и др.)

Пусть на множестве Х ={2, 4, 6, 8} задано отношение «меньше». Это означает, что для любых двух чисел из множества Х можно сказать, какое из них меньше: 2 < 4, 2< 6, 2< 8, 4< 6, 4< 8, 6< 8. Полученные неравенства можно записать в виде упорядоченных пар: (2; 4), (2;6), (2;8), (4;6), (4;8), (6;8). Но все эти пары есть элементы декартова произведения Х´Х.

Определение. Бинарным отношением на множестве Х называют всякое подмножество декартова произведения Х ´ Х.

Обозначаются отношения так же как и соответствия буквами: S, P, Т, R и др. Если R – отношение на множестве Х, то по определению, RÌX´X.

Элементы х и у находятся в отношении R кратко записывают (х,у)ÎR или хRу (читается: «элемент х находится в отношении R с элементом у»).

Отношения задаются также как и соответствия. Отличия касаются задания отношений при помощи графа.

Построим, например, граф отношения «меньше», заданного на множестве

Х = {2,4,6,8}. Для этого элементы множества Х изобразим точками (вершины графа), а отношение «меньше» – стрелками (ребра графа).

2 4

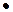
8 6

Отношение можно задать при помощи предложения с двумя переменными. Например, «число х меньше числа у» или в символической записи (если это возможно) «х < у». Отношение «х больше у на 3» можно записать в виде равенства х=у+3 (или х–у=3).

Для отношения R, заданного на множестве Х, всегда можно задать отношение R^–1, ему обратное. Оно определяется также, как соответствие, обратное данному.

Понятием отношения, обратного данному, часто пользуются при начальном обучении математике. Например, чтобы предупредить ошибку в выборе действия, с помощью которого решается задача: «У Пети 7 карандашей, что на 2 меньше, чем у Бори. Сколько карандашей у Бори?»– ее переформулируют: «У Пети 7 карандашей, а у Бори на 2 больше. Сколько карандашей у Бори?» Видим, что переформулировка свелась к замене отношения «меньше на 2» обратным ему отношением «больше на 2».

Дата добавления: 2014-01-06