Отношение порядка

Отношение эквивалентности. Взаимосвязь отношения эквивалентности с разбиением множества на классы

Лекция № 12

Если рассмотреть на множестве натуральных чисел отношение равенства, то можно заметить, что оно обладает свойствами рефлексивности, симметричности и транзитивности. Про такое отношение говорят, что оно является отношением эквивалентности.

Определение. Отношение R на множестве Х называется отношением эквивалентности, если оно одновременно обладает свойствами рефлексивности, симметричности и транзитивности.

Примерами отношений эквивалентности могут служить отношения равенства на множестве дробей, равенства геометрических фигур, отношение параллельности прямых и т. д.

Рассмотрим отношение равенства дробей, заданное на множестве Х={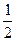; ; 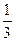; ;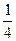;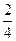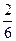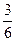}. Видим, что множество разбилось на три подмножества: {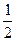,,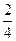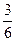}, {,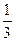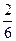}, {}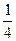. Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т.е. имеем разбиение множества Х на классы, каждый из которых состоит из равных между собой дробей.

Вообще, если на множестве Х задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно непересекающиеся подмножества (классы эквивалентности).

Верно и обратное утверждение: если какое-либо отношение, заданное на множестве X, порождает разбиение этого множества на классы, то оно является отношением эквивалентности.

Если отношение эквивалентности имеет название, то соответствующее название дается и классам.

Принцип разбиения множества на классы при помощи некоторого отношения эквивалентности является важным принципом математики. Отношения эквивалентности являются базой для формирования новых понятий (например, геометрических фигур) и для классифицирующей деятельности.

Слово «порядок» часто употребляется в обыденной речи. Можно говорить о порядке слов в предложении, о порядке выполнения действий в примере и т. д. При этом в слово «порядок» вкладывается такой смысл: оно означает, какой элемент того или иного множества за каким следует (или какой элемент какому предшествует).

Таким образом, интуитивное понятие порядка между элементами некоторого множества связано с заданием на этом множестве отношения «х следует за у» (или «х предшествует у»).

Определение. Отношение R на множестве Х называется отношением порядка (или отношением строгого порядка), если оно одновременно обладает свойствами антисимметричности и транзитивности.

Примерами отношений порядка могут служить: отношение «меньше» на множестве натуральных чисел, отношение «короче» на множестве отрезков, отношение «выше» на множестве людей, сравниваемых по росту.

Если отношение порядка обладает еще свойством связанности, то говорят, что оно является отношением линейного порядка.

Например, отношение «меньше» на множестве натуральных чисел является отношением линейного порядка.

Определение. Множество Х называется упорядоченным, если на нем задано отношение порядка.

Так, множество N натуральных чисел можно упорядочить, если задать на нем отношение «меньше».

Если отношение порядка, заданное на множестве Х, обладает свойством связанности, то оно линейно упорядочивает множество Х.

Например, множество натуральных чисел можно упорядочить и с помощью отношения «меньше», и с помощью отношения «кратно» – оба они являются отношениями порядка. Но отношение «меньше», в отличие от отношения «кратно», обладает еще и свойством связанности. Значит, отношение «меньше» упорядочивает множество натуральных чисел линейно.

Наряду с отношениями строгого порядка в математике рассматривают отношения нестрогого порядка.

Определение. Отношение R на множестве Х называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично и транзитивно.

Например, отношения: «х £ у», «не выше» на множестве людей, сравниваемых по росту, «быть делителем» на множестве натуральных чисел.

Не все отношения делятся на отношения эквивалентности и порядка. Существует большое число отношений, не являющиеся ни отношением эквивалентности, ни отношением порядка.

Дата добавления: 2014-01-06