Неравенство Чебышева. 1. Принцип практической уверенности

Закон больших чисел.

План лекции

Лекция 9

1. Принцип практической уверенности

3. Неравенство Чебышева

4. Теорема Ляпунова

Если в определенных условиях вероятность события очень мала, то при однократном их выполнении можно быть уверенным в том, что это событие не произойдет, и в практической деятельности поступать так, как будто оно является невозможным. Это и есть принцип практической уверенности.

Такую точную границу вероятности нельзя указать или вывести математически. Поэтому в каждом конкретном случае для каждого события мы должны устанавливать эту границу, исходя из того, насколько важны последствия при наступлении события, которое предполагается принять за невозможное.

Вероятность, которой решено пренебрегать в данном исследовании, называется уровнем значимости.

В статистике обычно рекомендуется пользоваться уровнем значимости 0,05 при предварительных исследованиях и 0.001 при окончательных выводах. Таким образом, в предварительных исследованиях за достоверные принимаются события, вероятности которых не менее 0,95, и при серьезных окончательных выводах, вероятности которых не менее 0,999.

Под законом больших чисел понимается совокупность предложений, в которых утверждается, что с вероятностью, как угодно близкой к единице, отклонение среднего арифметического достаточно большого числа случайных величин от постоянной величины-среднего арифметического их математических ожиданий –не превзойдет заданного как угодно малого числа ε >0.

Очень давно было замечено, что среднее арифметическое числовых характеристик некоторых признаков в большом числе однородных случайных явлений подвержено очень незначительным колебаниям, т.е. обладает устойчивостью. Теоретически объяснить такое поведение среднего можно с помощью закона больших чисел. Если будут выполнены некоторые общие условия относительно случайных величин, то устойчивость среднего арифметического - практически достоверное событие. Эти условия и составляют наиболее важное содержание закона больших чисел.

Вероятность отклонения СВ Х от ее математического ожидания подчиняется неравенству:

Р (|Х-а|>ε)≤ 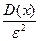,где D(Х) -дисперсия СВ Х.

События |Х-а|≤ε и |Х-а|>ε - противоположные, поэтому

Р (|Х-а|≤ε)≥1-Р(|Х-а| 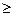ε)

или Р(|Х-а|≤ε)≥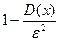 - это другая форма неравенства Чебышева.

Пример. Всхожесть семян некоторого растения составляет 70 %. Используя неравенство Чебышева, оценить вероятность того, что при посеве 10000 семян отклонение их всхожести непревзойден по абсолютной величин 0.01.

Решение. Частность события в n независимых испытаниях является случайной величиной. Ее математическое ожидание равно вероятности р наступления события в каждом испытании, а дисперсия равна pq/n. Поэтому неравенство Чебышева для частности события имеет вид:

Р (|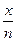-р|≤ ε) ≥ 1 -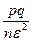

при р =0,7; q =0,3; ε =0,01; n =10000 имеем:

Р (|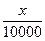- 0,7 |≤ 0,01 ) ≥ 1 - 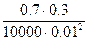=1-0,21=0,79.

Для использования неравенства Чебышева необходимо, чтобы 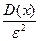<1.Это нужно для того, чтобы вероятность оставалась величиной неотрицательной.

Если у неотрицательной СВ Х существует математическое ожидание М(Х), то при любом положительном ξ имеет мест неравенство

Р (Х<ξ)≥ 1 -М(Х)/ξ (неравенство Маркова).

Пример. Средний срок службы мотора 4 года. Оценить снизу вероятность того, что данный мотор не прослужит более 20 лет.

Решение. СВ. Х – срок службы мотора. М (Х) =4. Требуется оценить Р (Х <20).Эту вероятность можно рассматривать как левую часть неравенства Маркова с ξ =20:

Р (Х <20)≥1-4/20=0,8.

Пример. Сумма всех вкладов в некотором сбербанке составляет 20000 руб., а вероятность того. что случайно взятый вклад не превышает 100 руб., равна 0,8. Что можно сказать о числе вкладчиков данного сбербанка?

Решение. СВ Х - величина случайно взятого вклада n -число вкладчиков; Р (Х <100)=0,8;

следовательно, Р (Х <100)≥1-20000/ n ·100; отсюда

0,8≥1-200/ n, или n ≤1000.

Дата добавления: 2014-01-06