Плотность вероятности непрерывной СВ

Плотностью вероятности φ(х) непрерывной СВ называется производная ее фyнкции распределения:

φ (х)=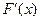

Наиболее важными являются непрерывные СВ, распределенные по нормальному закону (или закону Гаусса). В этом случае:

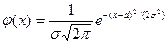, где а, 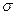-параметры.

Непрерывная СВ называется равномерно распределенной, если ее плотность вероятности имеет вид:

Рассмотрим предыдущий пример с минутной стрелкой. Продифференцируем функцию распределения:

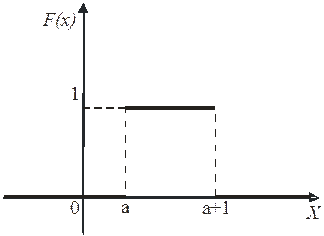
Непрерывная СВ называется распределенной по показательному закону, если она может принимать только неотрицательные значения, а ее плотность вероятности определяется равенством: 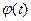= λе ^–λt, где t≥0, λ>0 -параметр.

Такие СВ обладают следующим свойством: если распределенный по показательному закону промежуток уже длился некоторое время, то это не влияет на закон распределения оставшейся части промежутка.

Теорема. Вероятность того, что непрерывная СВ Х примет какое-нибудь значение из интервала (а, b), равна

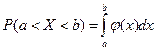
Из этой формулы можно получить, что 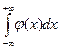=1

Вероятность того, что СВ примет какое-нибудь значение из интервала (-∞,+∞),равна единице, поскольку это событие достоверное. Это выражение называется условием нормировки.

Пример. Плотность вероятности СВ Х задана равенством 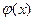= А/(1+х²) (-µ< х <+∞). Найти коэффициент А и вероятность того, что СВ Х примет значение из интервала (0;5).

Решение. Условие нормировки приводит к равенству:

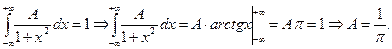
Таким образом, ;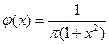

Функции φ(х) и F(x) взаимно определяют друг друга, поскольку:

.

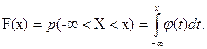Для полной характеристики СВ достаточно задать или функцию распределения, или плотность вероятности ее.

Кривой распределения непрерывной СВ называется график ее плотности вероятности.

Плотность вероятности любой СВ как производная неубывающей функции распределения является неотрицательной функцией при всех значениях аргумента. Для кривой распределения ось абсцисс служит асимптотой в обе или в одну сторону.

Дата добавления: 2014-01-06