План лекции. 1. Непрерывные случайные величины

Лекция 7

1. Непрерывные случайные величины.

2. Функция распределения случайной величины.

3. Плотность вероятности непрерывной случайной величины

Дискретная СВ характеризуются таблицей распределения. Однако задать СВ можно иначе, например, с помощью так называемой функции распределения. Этот способ задания СВ носит более общий характер. Он приводит к рассмотрению непрерывных СВ.

Рассмотрим событие, состоящее в том, что СВ Х примет значение Х<х. Обозначим вероятность этого как:

F(х)=P(X<x) (1)

Cлучайную величину можно считать полностью охарактеризованной, если для каждого х (-∞<х+∞) известно значение функции (1), которая называется функцией распределения СВ Х.

Функция распределения каждой дискретной СВ постоянна на интервалах, на которых нет ее значений, и имеет скачки в точках, соответствующих ее значениям. Скачки равны вероятностям, с которыми СВ принимает свои значения.

Теорема. Вероятность того, что СВ Х примет какое-нибудь значение в интервале х₁≤Х<х₂,равна приращению ее функции распределения F(x) на этом интервале:

Р(х₁≤Х<х₂)=F(x₂)-F(x₁) (2)

Теорема. Функция распределения любой СВ является неубывающей функцией, причем при изменении от -∞ до +∞ ее значения изменяются от 0 до 1.

Определение непрерывной СВ. СВ называется непрерывной, если ее функция распределения всюду непрерывна, а ее производная непрерывна во всех точках, за исключением, быть может, конечного числа точек на любом интервале.

Примеры непрерывных СВ: диаметр детали, которую токарь обтачивает до заданного размера; рост человека; дальность полета снаряда и.т.д.

Пусть построен график функции распределения F(x) некоторой непрерывной СВ.

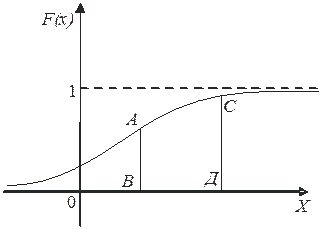
Ордината │АВ│ графика при Х=х₁ геометрически изображает вероятность того, что СВ примет какое-нибудь значение, меньшее х₁,а не вероятность того, что она примет значение х₂.

Можно показать, что вероятность Х=х₁ равна нулю. Событие Х=х₁ влечет событие

x₁-h≤X<x₁+h,где h>0. Поэтому Р(Х=х₁)≤Р(х₁-h≤X<x₁+h). Применим формулу (2):

P(X=x₁)≤F(x₁+h)-F(x₁-h).

Если h→0,то и правая часть неравенства стремится к нулю, т.к. F(x) непрерывна, следовательно:

, или Р(Х=х₁) ≤ 0, откуда Р(Х=х₁)= 0, поскольку вероятность любого события не может быть отрицательной.

Отсюда, в частности, следует, что для непрерывных СВ вероятности Р (х₁ ≤ Х < х₂),Р(х₁ < Х < х₂),

Р(х₁ < Х ≤ х₁) и Р(х₁ ≤ Х ≤ х₂) совпадают.

Если непрерывная СВ может принимать только значения в границах от а до b, где а и b -некоторые постоянные, то ее функция распределения равна нулю для всех значений х ≤ а и единице для всех значений х > b, поскольку события Х < х для любого х ≤ а являются в этом случае невозможными, а для любого х ≥ b -достоверными.

Пример. Минутная стрелка электрических часов передвигается скачками поминутно. Пусть часы показывают а минут. Тогда истинное время в данный момент является случайной величиной. Найти ее функцию распределения.

Решение. Очевидно, что функция распределения истинного времени равна нулю при х≤а и единице при х>а+1. Время течет равномерно. Вероятность того, что истинное время меньше а+0,5 минут, равна 0,5,т.к. одинаково вероятно, прошло ли после а менее или более полминуты. Вероятность того, что истинное время меньше, а+0,25 минут, равна 0,25 и.т.д. Функция распределения истинного времени имеет такое выражение:

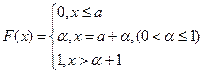
Она непрерывна всюду, а ее производная непрерывна во всех точках, за исключением х=а и х=а+1

СВ Х₁ и Х₂ называются независимыми, если для любых х₁ и х₂ события Х₁<х₁ и Х₂<х₂ независимы. Для вероятности произведения этих событий справедлива формула:

Р(Х₁<х₁; Х₂<х₂)=Р(Х₁<х₁)Р(Х₂<х₂).

Это неравенство можно переписать с помощью функций распределения F₁(x) и F₂(x):

P(X₁<x₁;X₂<x₂)=F(x₁)F(x₂).

Дата добавления: 2014-01-06