План лекции. 1. Математические операции над случайными величинами

Лекция 6

1. Математические операции над случайными величинами

2. Математическое ожидание дискретной случайной величины (свойства)

3. Дисперсия дискретной случайной величины (свойства)

4. Среднее квадратическое отклонение

Пусть СВ Х принимает значения х_i с вероятностями p_i=P(X=x_i), i=, a CB Y -значения y_j с вероятностями 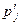=P(Y=y_j),j=.

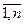Произведение kХ, где k -константа - это новая СВ, которая с теми же вероятностями, что и Х, принимает значения, равные произведениям СВ Х на k. Ее закон распределения имеет вид:

Значение	kх1	kх2	…	kхm
Вероятность	Р1	Р2	…	pm

Квадрат СВ Х, т.е. Х² -это новая СВ, которая с теми же вероятностями, что и СВ Х, принимает значения, равные квадратам ее значений.

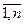Сумма СВ Х и Y- это новая СВ, которая принимает все значения вида x_i+y_j (i=; j=) с вероятностями , если СВ Х и Y независимы, то = .

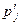Аналогично определяются разность и произведение СВ Х и Y. Разность СВ Х и Y -это новая СВ, которая принимает все значения вида -, а произведение - все значения вида с вероятностями, равными , а если X и Y независимы. то

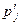
Пример. Следующая таблица определяет совместные распределение двух СВ Х₁ и Х₂ доходов фирмы в течение двух последовательных дней.

Х1	Х2
-10
-10	0,2	0,1	0,02
	0,03	0,3	0,05
	0,01	0,04	0,25

Определить: законы распределений СВ Х₁ и Х₂; закон распределения среднего дохода Y=(X₁+X₂)/2; закон распределения прироста дохода Z=X₂-X₁; являются ли СВ Х₁ и Х₂ независимыми.

Решение. СВ Х₁ может принимать три значения: -10,0 и 10. Каждое из них достигается при трех различных значениях Х₂. равных -10,0 и 10. Эти события несовместны, поэтому, например, Х₁=-10 имеет вероятность:

Р(Х₁= -10)=Р(Х₁=-10/Х₂=-10)+Р(Х₁=-10/Х₂=0)+Р(Х₁=-10/Х₂=10)=0,2+0,1+0,02=0,32,

т.е. вероятность данного значения Х₁ получаем суммированием первой строки таблицы. Аналогично вероятности других значений Х₁ получаем суммированием вероятностей других строк таблицы, получаем закон распределения Х₁:

Х1	-10
Р(Х1)	0,32	0,38	0.30

Вероятности различных значений Х₂ получаем суммированием значений соответствующих столбцов:

Х2	-10
Р (Х2)	0,24	0,44	0,32

Закон распределения среднего дохода Y начнем с рассмотрения значений, которые принимает эта СВ в каждой клетке совместного распределения Х₁ и Х₂:

-10	-5
-5

Следовательно, СВ Y=(X₁+X₂)/2 принимает значения -10,-5,0,5 и 10. События в отдельных клетках совместного распределения несовместны, поэтому вероятность того или иного значения СВ Y получаем суммированием вероятностей по всем клеткам, где СВ Y принимает одно и то же значение. Например, Р (Y=0) =0,02+0,30+0,01=0,33 и.т.д. Закон распределения имеет вид:

Y	-10	-5
P(Y)	0,2	0,13	0,33	0,09	0,25

CB Z принимает значения -20,-10,0,10,20. Их вероятности также получаем сложением вероятностей тех клеток первоначальной таблицы, в которых величина Z принимает фиксированные значения:

Z	-20	-10
P(Z)	0,01	0,07	0,75	0,15	0,02

Для ответа на вопрос, являются ли СВ Х₁ и Х₂ независимыми, надо проверить равенства

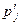=, или Р(x_i;X₂=y_j)=P(X₁=x_i)·P(X₂=y_j)

для всех сочетании значений Х₁ и Х₂. Однако мы видим, что

Р(Х₁=-10;Х₂=-10)≠Р(Х₁=-10)·Р(Х₂₌-10),поскольку 0,2≠0,32·0,24.

Это достаточно, чтобы делать вывод о том. Что СВ Х₁ и Х₂ не являются независимыми.

Дата добавления: 2014-01-06