Независимость случайных величин

Дискретные СВ Х и Y называются независимыми, если при любых i и j события Х=х_i и

Y=у_j (i=; j=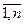) независимы.

Пример: независимыми являются СВ Х₁ и Х_{2 ,}выражающие размер выигрыша на приобретенные два билета(соответственно на первый и второй)денежно-вещевой лотереи различных выпусков. Если на первый билет выпал выигрыш, т.е. Х₁ приняла некоторое значение, то закон распределения Х₂ не изменится. Если же Х₁ и Х₂ означают выигрыш на два купленных билета лотереи одного и того же выпуска, то Х₁ и Х₂ являются зависимыми СВ.

Пусть имеются две СВ: Х может принимать значенияx x_i с вероятностями p_i (i=), Y -значения у_j с вероятностями p_j(j=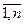). Рассмотрим событие С_ij, являющиеся произведением двух событий: Х=х_i и Y=у_j. Вероятность этого события:

p_{ij =} P(X=x_i;Y=у_j)

Рассмотрим условную вероятность события Y=у_j относительно события Х=x_i:

P(Y=y_j / X=xi) =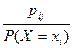

Совокупность вероятностей Р (Y=y_j /X=x_i) при всех j=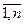 и значений СВ Y составляет ее условный закон распределения в предположении, что СВ Х приняла значение x_i. Из последней формулы следует, что

р_ij=P (X=x_i;Y=y_j)=p(X=x_i)·P(Y=y_j /X=x_i)

Обозначим через А событие Х=x_i. Его вероятность можно представить в виде

P(A)=P(X=x_i)=p_i=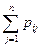=p_i1+p_i2+...+p_in, поскольку правую часть можно записать так:

P(X=x_i; Y=y₁) + P(X=x_i; Y=y₂) +...+P(X=x_i; Y=y_n)

События в скобках несовместны, поэтому последняя сумма выражает вероятность события В, состоящего в том, что произойдет какое-либо одно из n событий (X=x_i; Y=y_j), j=.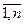

Покажем, что события А и В эквивалентны. Пусть имело место событие А. Поскольку СВ Y обязательно примет одно из своих возможных значений, то произойдет одно из событий (X=x_i;Y=y_j), j=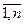, т.е. наступит событие В. Пусть произойдет событие В, т.е. имеет место одно из событий (X=x_i;Y=y_j), j=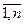, следовательно, произошло и событие X=x_i, т.е. А. Из эквивалентности А и В следует равенство их вероятностей и справедливость последнего равенства.

Аналогично можно доказать, что

=

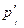Если СВ Х и Y независимы, то для вероятности события С_ij (i=; j=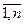)имеет место соотношение:

=

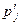
Дата добавления: 2014-01-06