Дисперсия дискретной СВ и ее свойства

Дисперсия СВ служит мерой рассеивания (разброса) данной СВ по отношению к ее математическому ожиданию. Она определяется как квадрат отклонения данной СВ от ее математического ожидания:

D(Х)=М(Х-М(Х))² (1)

или, если a -математическое ожидание СВ Х,

D (Х)=(х₁-а)²р₁+(х₂-а)²р₂+…+(х_m-а)²·р_m=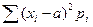 (2)

Средним квадратическим отклонением (с.к.о.), или стандартным отклонением σ(Х) (или просто σ) СВ Х называется арифметическое значение корня квадратного из ее дисперсии:

σ (Х)=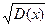 (3)

Если дисперсия СВ Х мала, то малы и все члены суммы (2),поскольку они не отрицательны. Поэтому, если существуют x_i. Сильно отклоняющиеся от математического ожидания, то все они маловероятны. Если же дисперсия велика, это указывает на существование значений СВ, которые сильно отклоняются от ее математического ожидания, причем не все они маловероятны.

Дисперсия СВ - постоянная величина. Она является ее второй обобщающей теоретико-вероятностной характеристикой.

С.к.о. характеризует степень отклонения СВ от ее математического ожидания и имеет размерность значений СВ.

Свойства дисперсии:

1.Дисперсия постоянной величины равна нулю:

D (С)=0, С=const.

2.Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат:

D(kХ)=k²D (Х)

3.Дисперсия может быть рассчитана по формуле:

D (Х)=М(Х²)-М²(Х)

4.Дисперсия алгебраической суммы конечного числа независимых СВ равна сумме их дисперсий. В частности, для двух СВ Х и Y:

D (Х±Y)=D(Х)+D(Y), Х,Y -независимы.

Следствие. С.к.о. суммы конечного числа независимых СВ равно корню квадратному из суммы квадратов их с.к.о.:

=.

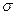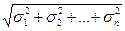Дата добавления: 2014-01-06