Глоссарий. Первообразная функции f(x) на промежутке Х – это такая функция F(x), производная которой в каждой точке х этого промежутка равна f(x)

Первообразная функции f(x) на промежутке Х – это такая функция F(x), производная которой в каждой точке х этого промежутка равна f(x).

Неопределенный интеграл от функции f(x) – это совокупность всех первообразных для функции f(x) на соответствующем промежутке.

Интегральная сумма для функции f(x) на [a,b] – это сумма вида , где

Определенный интеграл – предел последовательности интегральных сумм при 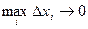, если этот предел существует, конечен и не зависит от способа выбора точек .

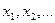Обыкновенное дифференциальное уравнение (ОДУ) – это уравнение вида 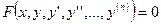, связывающее аргумент, неизвестную функцию и её производные (в неявной форме). В явной форме оно разрешено относительно старшей производной: .

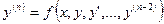Общее решение ОДУ n – гопорядка имеет вид 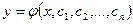и является функцией переменной х и n произвольных констант С₁, С₂,…, С_n.

Частное решение ОДУ n – го порядка получается при подстановке в общее решение некоторых конкретных числовых значений С₁, С₂,…, С_n.

Неполное ДУ – это ОДУ 1 порядка 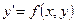в случае, если функция f явно зависит либо только от х, либо только от у.

Уравнение с разделяющимися переменными – это ОДУ вида 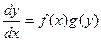или .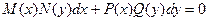

Однородное ДУ 1 порядка – уравнение вида .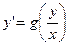

Линейное ДУ 1 порядка имеет вид .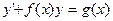

Линейные ДУ 2 порядка с постоянными коэффициентами имеет вид 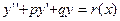, где p,q – константы, r(x) – функция.

Числовой ряд – это бесконечная сумма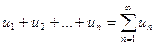

Сумма числового ряда – это предел последовательности его частичных сумм.

Абсолютно сходящийся ряд – это ряд, который сходится сам, и сходится также ряд из абсолютных величин его членов.

Условно сходящийся ряд – это ряд, который сам сходится, а ряд из абсолютных величин его членов расходится.

Степенные ряды – это ряды, членами которых являются степенные функции.

Область сходимости степенного ряда – это совокупность тех значений х, при которых степенной ряд сходится.

Линия уровня функции двух переменных - это множество точек на плоскости, в которых функция принимает одно и то же значение С.

Частная производная функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению этой независимой переменной при стремлении последнего к нулю, если этот предел существует.

Дифференциал функции нескольких переменных – сумма произведений частных производных этой функции на приращения соответствующих независимых переменных.

Градиент функции - это вектор с координатами .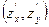

Достоверное событие - событие, которое происходит при каждом испытание.

Невозможное событие - событие, которое не может произойти не при одном испытании.

Случайное событие - событие, которое в данном испытании может произойти, а может и не произойти.

Сумма событий А и В называется такое событие А+В, которое состоится при появлении или события А, или события В, или обоих событий вместе.

Произведение событий - произведением событий А и В называется событие АВ, которое происходит при одновременном наступлении обоих событий.

Разность событий: событие, которое состоится, если событие А произойдет, а событие В не произойдет, называется разностью событий А и В и обозначается А - В.

Эквивалентность событий - если имеет место одновременно и АÌ В, и ВÌ А, то события А и В называются равносильными (эквивалентными). В этом случае пишут А=В.

Несовместные события - События А и В называются несовместными, если их совместное наступление невозможно, т.е. А В = ø

Противоположные события: два несовместных события А и В называются противоположными, если при всякой реализации комплекса условий одно из них обязательно происходит.

Законы де Моргана - это выражения 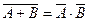и

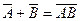
Единственно возможныесобытия: события А 1, А 2,..., А n называются единственно возможными, если в результате испытания приходит какое – либо одно и только одно из этих событий. Говорят также, что эти события образуют полную группу.

Пространство элементарных событий: Каждое испытание можно описать с помощью событий, которые являются несовместными и единственно возможными. Эти события называются исходами испытания, или элементарными событиями. Эти события называются исходами испытания, или элементарными событиями.

Равновозможные события: события называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Вероятность: вероятностью события А называется отношение числа исходов, благоприятных событию А, к числу всех исходов испытания.

Относительная частота: относительной частотой события А называется отношение числа испытаний, в которых это событие появилось, к общему числу фактически появилось, к общему числу фактически произведенных испытаний, т.е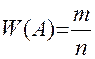

Независимые события: события А и В являются независимыми, если имеет место равенство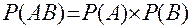

Случайная величина: случайной величиной называется переменная, которая может принимать те или иные значения в зависимости от различных обстоятельств.

Математическое ожидание дискретной случайной величины - это сумма произведений всех ее значений на соответствующие вероятности:

М(Х)=х₁р₁+х₂р₂+…=х_mp_m=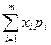

Математическое ожидание непрерывной случайной величины: математическим ожиданием М (Х) непрерывной СВ Х с плотностью вероятности φ(х) называется величина интеграла:

М (Х)=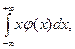

если он сходится абсолютно.

Дисперсия дискретной случайной величины определяется как квадрат отклонения данной СВ от ее математического ожидания:

D (Х)=М (Х-М(Х))²

или, если a -математическое ожидание СВ Х,

D (Х)=(х₁-а)²р₁+(х₂-а)²р₂+…+(х_m-а)²·р_m=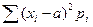

Дисперсия непрерывной случайной величины: величина интеграла D(Х)=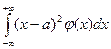, где а = М(Х),если он сходится.

Среднее квадратическое отклонение: средним квадратическим отклонением (с.к.о.), или стандартным отклонением σ(Х) (или просто σ) СВ Х называется арифметическое значение корня квадратного из ее дисперсии: σ (Х)=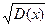

Функция распределения случайной величины: это функция F(x), равная вероятности того, что случайная величина Х примет значение, меньшее х.

Плотность вероятности: плотностью вероятности φ(х) непрерывной СВ называется производная ее фyнкции распределения: φ (х)=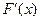

Дата добавления: 2014-01-06