Исходные данные и результаты расчета скользящей средней, ц/га

Объем производства продукции предприятия (по кварталам) в сопоставимых ценах, руб.

Объем производства продукции предприятия (по месяцам) в сопоставимых ценах, млн. руб.

Месяц	Объем производства	Месяц	Объем производства
Январь	5,1	Июль	5,6
Февраль	5,4	Август	5,9
Март	5,2	Сентябрь	6,1
Апрель	5,3	Октябрь	6,0
Май	5,6	Ноябрь	5,9
Июнь	5,8	Декабрь	6,2

Различные направления изменений уровней ряда по отдель­ным месяцам затрудняют выводы об основной тенденции про­изводства. Если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск продукции по кварталам (табл. 7.8), т. е. укрупнить интервалы, то решение задачи упрощается.

Таблица 7.8

Квартал	За квартал	В среднем за месяц
I	15,7	5,23
II	16,7	5,57
III	17,6	5,87
IV	18,1	6,03

После укрупнения интервалов основная тенденция роста производства стала очевидной:

5,23 < 5,57 < 5,87 < 6,03 млн. руб.

Ø Выявление основной тенденции может осуществляться также методом скользящей (подвижной) средней. Сущность его заключается в том, что исчисляется средний уровень из опреде­ленного числа, обычно нечетного (3, 5, 7 и т.д.), первых по сче­ту уровней ряда, затем - из такого же числа уровней, но начи­ная со второго по счету, далее — начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, пере­двигаясь на один срок.

Расчет скользящей средней по данным об урожайности зер­новых культур приведен в табл. 7.9.

Сглаженный ряд урожайности по трехлетиям короче факти­ческого на один член ряда в начале и в конце, по пятилетиям - на два члена в начале и конце ряда. Он меньше, чем фактиче­ский подвержен колебаниям из-за случайных причин, и четче, в виде некоторой плавной линии на графике (рис. 7.4), выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития.

Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следователь­но, потеря информации.

Рассмотренные приемы сглаживания динамических рядов (укрупнение интервалов и метод скользящей средней) дают воз­можность определить лишь общую тенденцию развития явле­ния, более или менее освобожденную от случайных и волнооб­разных колебаний. Однако получить обобщенную статистиче­скую модель тренда посредством этих методов нельзя.

Таблица 7.9

Год	Фактический уровень урожайности, ц.	Скользящая средняя
Трехлетняя	Пятилетняя
	15,4	_	_
	14,0		_
	17,6		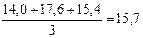14,7
	15,4		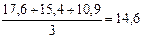15,1
	10,9	14,6	15,2
	17,5	14,5	17,1
	15,0	17,0	16,8
	18,5	15,9	17,6
	14,2	15,9	_
	14,9	_	_
	∑y = 153,4

Ø Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во вре­мени, используется аналитическое выравнивание ряда динамики.

Основным содержанием метода аналитического выравнива­ния в рядах динамики является то, что общая тенденция разви­тия рассчитывается как функция времени:

,

где — уровни динамического ряда, вычисленные по соответст­вующему аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней произ­водится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимиру­ет) основную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме).

Например, простейшими моделями (формулами), выражаю­щими тенденцию развития, являются:

линейная функция – прямая = а₀+ a₁t

где а₀, a₁ – параметры уравнения; t – время;

показательная функция = а₀a₁^t;

степенная функция – кривая второго порядка (парабола)

=а₀+ a₁t + a₂t².

В тех случаях, когда требуется особо точное изучение тен­денции развития (например, модели тренда для прогнозирова­ния), при выборе вида адекватной функции можно использовать специальные критерии математической статистики.

Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принима­ется точка минимума суммы квадратов отклонений между тео­ретическими и эмпирическими уровнями:

(7.17)

где - выровненные (расчетные) уровни; у_i - фактические уровни.

Параметры уравнения а_i, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выровненные уровни. Таким образом, выравнивание ряда динамики заключается в замене фактических уровней у_i плавно изменяю­щимися уровнями , наилучшим образом аппроксимирующи­ми статистические данные.

• Выравнивание по прямой используется, как правило, в тех случаях, когда абсолютные приросты практически посто­янны, т. е. когда уровни изменяются в арифметической прогрессии (или близко к ней).

• Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометриче­ской прогрессии, т. е. когда цепные коэффициенты рос­та практически постоянны.

Рассмотрим «технику» выравнивания ряда динамики по пря­мой: = а₀+ a₁t. Параметры а₀, a₁ согласно методу наимень­ших квадратов находятся решением следующей системы нор­мальных уравнений, полученной путем алгебраического преобра­зования условия (7.17):

_(7.18)

где у — фактические (эмпирические) уровни ряда; t — время (по­рядковый номер периода или момента времени).

Расчет параметров значительно упрощается, если за начало отсчета времени (t = 0) принять центральный интервал (момент).

При четном числе уровней (например, 6), значения t — ус­ловного обозначения времени будут такими (это равнозначно из­мерению времени не в годах, а в полугодиях):

1995 г. 1996 г. 1997 г. 1998 г. 1999 г. 2000 г.

-5 -3 -1 +1 +3 +5

При нечетном числе уровней (например, 7) значения уста­навливаются по-другому:

1994 г. 1995 г. 1996 г 1997 г. 1998 г. 1999 г. 2000 г.
-3 -2 -1 0 +1 +2 +3

В обоих случаях ∑ t = 0, так что система нормальных урав­нений (7.18) принимает вид:

(7.19)

Из первого уравнения 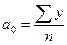(7.20)

Из второго уравнения (7.21)

Проиллюстрируем на примере урожайности зерновых куль­тур (см. табл. 7.9, расчетные значения — табл. 7.10) выравнива­ние ряда динамики по прямой.

Для выравнивания данного ряда используем линейную трендовую модель - уравнение прямой: = а₀+ a₁t. В нашем при­мере п =10 — четное число.

Параметры а₀ и а₁ искомого уравнения прямой исчислим по формулам (7.20) и (7.21).

Таблица 7.10

Дата добавления: 2014-01-06