Выработка продукции на предприятии

Продукция, ед. изм.	Выработано продукции, тыс.	Цена за единицу, руб.
	q0	q1	p0	p1
	2	3	4	5	6
А, кг					1,00
Б, м					1,20
В, шт.					0,70

Индивидуальные (однотоварные) индексы (гр.6 табл.8.1) пока­зывают, что в отчетном периоде выпуск продукции А остался на уровне базисного периода, продукции Б — увеличился на 20%, а выпуск продукции В снизился на 30%.

1. Для того чтобы на основе данных табл. 8.1 об изменениях выпуска всей продукции, используется общий индекс физического объема продукции — формула (8.4):

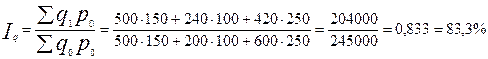
Следовательно, физический объем всей продукции в отчетном пе­риоде составляет 83,3% от его уровня в базисном периоде, он снизился за это время на 16,7%, т. е. (0,833 100 - 100).

Вычитая из числителя знаменатель, находим абсолютный при­рост (снижение) стоимости продукции в неизменных ценах,

=204000-245000 = -41000, т.е.-40млн руб.

Следовательно, в отчетном периоде стоимость продукции умень­шилась в абсолютном выражении на 41 млн руб. (только за счет сни­жения на 16,7% физического объема производства продукции).

2. Сделав расчет индекса стоимости продукции по формуле (8.3), найдем, как изменился за этот период общий объем продук­ции в фактических ценах (т.е с учетом изменения цен):

Общий выпуск продукции (стоимость) в фактических ценах в текущем периоде составил 90,8% ее выпуска в базисном периоде, или с учетом изменения цен снизился на 9,2%, т.е. (0,908 • 100 - 100); выпуск продукции уменьшился в абсолютном выражении на 22,6 тыс. руб., ∑ q₁ p₀ -∑ q₀ p_0.

Значение общего индекса Ipq зависит от изменения двух ин­дексируемых величин: количество товаров (q₁,q₀) и цен (p₁, p₀).

Она характеризует изменение объема продукции и в целом про­дукции в целом, т.е. отражает одновременное влияние обоих фак­торов — изменение и количеств товаров и изменение уровня цен.

Этот индекс чаще вычисляется в торговле, когда необходимо знать изменение товарооборота в фактических ценах. В промыш­ленности же преимущественно исчисляется индекс физического объема продукции в сопоставимых, фиксированных ценах, по­зволяющих определить динамику выпускаемой продукции.

Агрегатный способ исчисления общих индексов в статистике является основным наиболее распространенным, вместе с тем применяется и другой способ расчета общих индексов как сред­них из соответствующих индивидуальных индексов. К исчисле­нию таких средневзвешенных индексов прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчи­тать общий агрегатный индекс. Так, если неизвестны количества произведенных отдельных видов продукции в натуральных измерителях, но известны индивидуальные индексы и стоимость продукции базисного периода (p₀q₀), можно определить средний арифметический индекс физического объема продукции.

Исходной базой построения средневзвешенного индекса физического объема продукции служит его агрегатная форма, см. формулу (8.4):

Из имеющихся данных непосредственно можно только по­лучить знаменатель этой формулы. Для нахождения числителя используем формулу индивидуального индекса объема продукции , из которой следует, что q_{1 =} i_q ∙ q_0. Подставляя данное выражение в числитель агрегатной формы, получаем общий индекс физического объема в форме среднего арифметического индекса физического объема продукции, где весами служит стоимость отдельных видов продукции в базисном периоде(q₀ p₀):

(8.7)

При выборе весов следует иметь в виду, что средний индекс должен быть тождественен агрегатному, который является ос­новной формой индекса.

Если известны данные, позволяющие исчислить только чис­литель агрегатного индекса физического объема по формуле (8.4), то, аналогично выражая продукцию базисного периода как

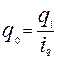, производим замену в знаменателе агрегатной формы. В результате получаем общий индекс физического объема в форме среднего гармонического взвешенного индекса физического объема продукции, где весами служит стоимость продукции отчетного периода в базисных(или сопоставимых) ценах(q₁ p₀):

(8.8)

В форме средней гармонической взвешенной индекс физи­ческого объема используется только в аналитических целях.

Следовательно, применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического или среднего гармонического) зависит от имеющихся в нашем распоряжении конкретных данных и цели исследования.

Так, при наличии данных о стоимости продукции в сопоставимых ценах в базисном периоде общий индекс физического объема продукции должен рассчитываться как средний арифметический взвешенный (см. табл. 8.2):

Задача 2. Имеются данные выпуска продукции по заводу строи­тельных пластмасс (табл. 8.2.):

Таблица 8.2

Вид продукции	Выпуск продукции в I квар­тале, млн. руб.	Изменение объема производства во II квартале в нату­ральном выражении, %
Пленка Пеноплен Линолиум		+ 10 -10 -25

Определить: сводную оценку изменения объема производства продукции (в натуральном выражении)

Решение:

1. Из условия следует, что индивидуальные индексы по видам продукции имеют следующие значения:

i’=1,1; i”=0,9; i’’’=0,75.

2. Индекс физического объема продукции:

Следовательно, объем производства в натуральном выражении во втором квартале по сравнению с первым уменьшился на 10%.

8.3. Общие индексы качественных показателей

Каждый качественный показатель связан с тем или иным объемным показателем, в расчете на единицу которого он ис­числяется. Так, с объемом произведенной (проданной) продук­ции связаны такие качественные показатели, как цена р, себе­стоимость z и трудоемкость t.

В условиях рыночных отношений в экономике особое место среди индексов качественных показателей отводится индексу цен. С помощью индекса потребительских цен (ИПЦ) осуществляются оценка динамики цен на товары производственного и непроизводственного потребления, пересчет важнейших стоимо­стных показателей СНС из фактических цен в сопоставимые. Индекс потребительских цен является общим измерителем ин­фляции, используется при корректировке законодательно уста­навливаемого минимального размера оплаты труда, установле­нии ставок налогов и т.д.

Рассмотрим принципы построения агрегатных индексов качественных показателей на примере индекса цен.

Поскольку этот индекс характеризует изменение цен, индек­сируемой величиной в нем будет цена товара. Влияние количества проданных товаров должно быть устранено, а это возможно только в том случае, если количество продаваемых товаров не­изменно в оба периода, т. е. количество товаров одного из пе­риодов принято в качестве весов индекса.

Вопрос о том, количество проданных товаров какого перио­да (текущего или базисного) следует взять в качестве весов при построении агрегатного индекса, решается исходя из сферы его применения.

При построении индекса цен в качестве весов индекса обыч­но берут количество товаров, проданных в текущем (отчетном) периоде. Это объясняется тем, что такое исчисление индекса цен позволяет определить не только относительное изменение цен (путем деления числителя индекса ∑ q₁ p₁ на его знамена­тель ∑ q₁ p₀ ), но и абсолютную экономию (—) или абсолютный перерасход (+) денежных средств покупателей в результате из­менения цен на эти товары (как разность между числителем и знаменателем индекса):

Агрегатный индекс цен с отчетными весами впервые предло­жен в 1874 г. немецким экономистом Г.Пааше и носит его имя. Формула агрегатного индекса цен Пааше:

(8.9)

где ∑ q₁ p₁ — фактическая стоимость продукции (товарооборот) от­четного периода;

∑ q₁ p₀ — условная стоимость товаров, реализованных в отчет­ном периоде по базисным ценам.

Индекс цен Пааше показывает, во сколько раз возрос (уменьшился) в среднем уровень цен на массу товара, реализо­ванную в отчетном периоде, или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базис­ным периодом.

Если из значения индекса цен I_Р вычесть 100%, т.е. (l_p -100),то

разность покажет на сколько процентов в среднем возрос (уменьшил­ся) за это время уровень цен на массу товаров, реализованную в от­четном периоде.

При таком методе, рассчитав индекс цен по формуле (8.9), можно подсчитать экономический эффект от изменения цен.

Однако надо отметить, что указанный выбор весов при по­строении агрегатного индекса цен нельзя считать обязательным во всех случаях. В статистике многие задачи могут и должны ре­шаться по-разному в зависимости от конкретной цели и особен­ностей исследования. Проиллюстрируем это следующими рассу­ждениями. Как известно, во время экономического кризиса рез­ко растут цены. В результате ряд продуктов выпадает из потреб­ления населения, особенно малообеспеченных. Допустим, что в условном базисном периоде в состав потребления входило 30 наименований продуктов (q₀ = 30), а в текущем периоде -

только 25 наименований (q₁ = 25) Очевидно, что при такой си­туации индекс цен, рассчитанный пo q₁, неправильно отразит

изменение цен на те продукты, которые выпали из потребления из-за чрезмерного повышения цен.

Поэтому в подобных случаях более правильно отразит изме­нение цен индекс, построенный по продукции базисного перио­да (предложен в 1864 г. немецким экономистом Э. Ласпейресом и носит его имя).

Формула агрегатного индекса цен Ласпейреса:

(8.10)

Итак, агрегатные индексы цен с текущими весами определя­ются по формуле (8.9), с базисными весами по формуле (8.10). Эти индексы не идентичны. Значения индексов цен Пааше и Ласпейреса для одних и тех же данных не совпадают, так как имеют различное экономическое содержание.

► Индекс Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде, и фактическую экономию (перерасход) от изме­нения цен, т.е. индекс цен Пааше показывает, на сколько това­ры в отчетном периоде стали дороже (дешевле), чем в базисном.

► Экономическое содержание индекса Ласпейреса другое: он показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде, и экономию (перерасход), ко­торую можно было бы получить от изменения цен, т. е. условную экономию (перерасход). Иначе говоря, индекс цен Ласпейреса по­казывает во сколько раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде. Поэтому применение формулы Ласпейреса ограничено особыми условиями исследования (например, при прогнозировании объе­ма товарооборота, в связи с намечаемыми изменениями цен на товары в предстоящем периоде).

При выборе периода, на основе которого производится взве­шивание, нужно иметь в виду два противоречащих друг другу требования:

• задачи изучения структуры и динамики цен требуют, чтобы расчеты показателей цен проводились в течение достаточно длительного периода на одной и той же базе сравнения;

• непрерывно происходящие изменения в структуре произ­водства и потребления, в соотношении цен на отдельные продукты, появление новых продуктов и исчезновение старых, изменение качества продуктов требуют возможно более частого изменения базисного периода.

До перехода к рыночным отношениям отечественная стати­стика отдавала предпочтение индексу цен Пааше. В условиях же высокой инфляции взвешивание по весам отчетного периода (индекс Пааше) требует ежегодного (ежеквартального, ежемесяч­ного) пересчета информации для формирования системы весов, что связано с большими затратами времени, материальных и тру­довых ресурсов, поэтому, начиная с 1991 г., органы государст­венной статистики России определяют изменение общего уровня цен на товары и услуги по формуле Ласпейреса, которой отдается предпочтение и в зарубежной статистике. Наблюдение за изме­нением цен (тарифов) проводят на территории всех субъектов Российской Федерации.

Для характеристики динамики цен на потребительском уров­не рассчитывается сводный индекс потребительских цен (ИПЦ), который отражает динамику цен конечного потребления.

«Идеальный» индекс цен Фишера (по имени американского экономиста И.Фишера) представляет собой среднюю геометри­ческую из произведения двух агрегатных индексов цен Ласпейреса и Пааше:

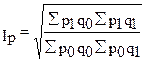(8.11)

Идеальность формулы заключается в том, что индекс являет­ся обратимым во времени, т.е. при перестановке базисного и отчетного периодов полученный «обратный» индекс — это ве­личина обратная величине первоначального индекса (этому ус­ловию отвечает любой индивидуальный индекс).

Однако геометрическая форма индекса имеет принципиаль­ный недостаток: она лишена конкретного экономического со­держания. Так, в отличие от агрегатного индекса Пааше и Ласпейреса разность между числителем и знаменателем не покажет никакой реальной экономии (или потерь) из-за изменения цен.

Индекс Фишера в силу сложности расчета и трудности эко­номической интерпритации на практике используется довольно редко, чаще всего — при исчислении индексов цен за длитель­ный период времени для сглаживания тенденций в структуре и составе объема продукции, в которых происходят значительные изменения.

Рассмотрим расчет индексов цен Пааше и Ласпейреса по данным табл.8.3.

Задача 3. Имеются данные о продаже товаров на рынке (табл.8.3.).

Определить:

1) индекс цен Пааше;

2) индекс цен Ласпейреса;

3) индекс физического объема продукции.

Таблица 8.3

Дата добавления: 2014-01-06