И фазами

Сложение одночастотных колебаний с разными амплитудами

Представим суперпозицию двух колебани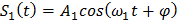й

, и

с произвольными амплитудами и начальными фазами на векторной диаграмме (рис. 16), используя некоторую ось отсчета ОВ. Определим амплитуду и фазу суммарного колебания, имея в виду, что частота ω₁ неизменна.

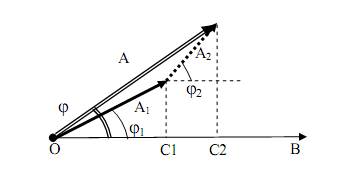
Рис. 16. Сложение произвольных колебаний

Из диаграммы следует

(9)

Возведем в квадрат выражения (9) и сложим их, тогда получим

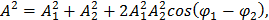
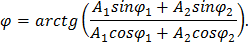
Из последних выражений следует:

1) Квадрат амплитуды суммарного колебания всегда положителен и зависит от соотношения амплитуд и начальных фаз двух колебаний.

2) Фаза суммарного колебания также определяется амлитудами и начальными фазами колебаний S₁(t) и S₂(t).

3) Частота результирующего колебания не изменяется.

В случае синфазного сложения колебаний амплитудные различия двух колебаний играют значительную роль. При этом амплитуда суммарного колебания будет равна сумме амплитуд двух колебаний (рис. 17, а)

(12)

В этом случае по суммарному колебанию сложно судить о вкладе каждой из амплитуд двух колебаний. На рис. 17, б приведена векторная диаграмма суперпозиции двух колебаний относительно заданной оси ОВ.

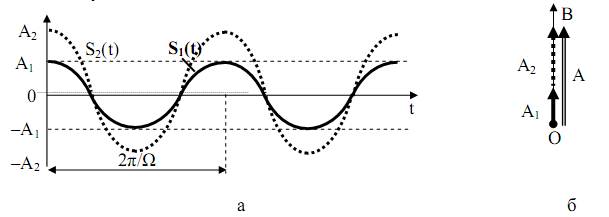
Рис. 17. Синфазное сложение колебаний

При противофазном сложении колебаний амплитудное значение суммарного колебания будет определяться разностью амплитуд двух колебаний т.к.

(13)

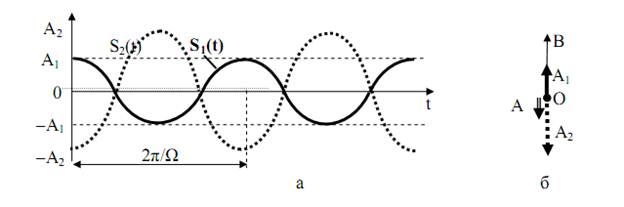
Рис. 18. Противофазное сложение колебаний

На рис. 18, б приведена векторная диаграмма суперпозиции двух противофазных колебаний относительно заданной оси ОВ. Рассмотрим случай когда (рис. 19, а)

(14)

Из (10) следует, что амплитуда суммарного колебания при этом будет определяться как 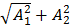. Это видно из диаграммы, приведенной на рис. 19, б. Фазовая компонента суммарного колебания будет зависить от соотношения амплитуд двух колебаний и изменяться в пределах от 0^о до 90^о.

Рис. 19. Сложение колебаний с фазовым разносом π/₂

Если второе колебание сдвинуто на 3π/2 (рис. 20, а), амплитуда суммарного колебания равна 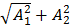, а его фаза в зависимости от соотношения амплитуд двух колебаний изменяется в пределах от 0^о до –90^о.

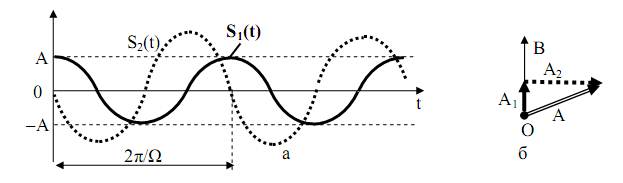
Рис. 20. Сложение колебаний с фазовым разносом 3π/₂

При сложении двух колебаний с произвольным фазовым набегом квадрат амплитуды суммарного колебания будет изменяться по функции, приведенной на рис. 21.

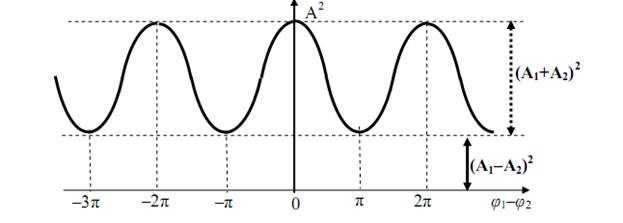
Рис. 21. Зависимость квадрата амплитуды суммарного колебания от разности фаз двух колебаний

Из графика следует, что квадрат амплитуды результирующего колебания изменяется в интервале от (A₁ + A₂)² до (A₁ – A₂)². Максимумам функции соответствуют фазовые различия , а минимумам , где k = 0, 1, 2…

Дата добавления: 2014-01-07