Гармонический анализ периодических колебаний

Аналитическое описание периодических колебаний

Для описания сложных колебаний, под которыми будем понимать колебания, отличающиеся от гармонических, используется система базисных функций. Важное значение здесь приобретают ортогональные системы функций.

Напомним из математики, что система действительных функций

является ортогональной на интервале [a, b], если

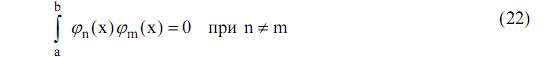
при условии, что ни одна из этих функций

Величина, определяемая как

называется нормой.

Когда функции 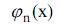непрерывны, то произвольная кусочно-линейная функция может быть представлена в виде ряда

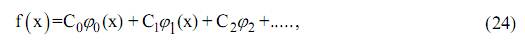
если коэффициенты этого ряда определяются как

то ряд (24) называется обобщенным рядом Фурье.

Для разложения периодических колебаний в ряд Фурье используются тригонометрические

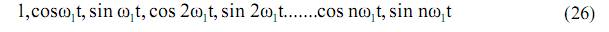
или комплексные функции

где 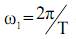– частота первой гармоники.

Система (26) приводит к тригонометрической форме записи ряда Фурье, а (27) – комплексной. Воспользуемся сначала системой (27) и перепишем ряд (24) для произвольного периодического колебания S(t) в виде

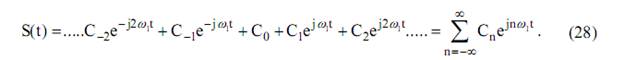
Определим норму функции (27) для периодического колебания

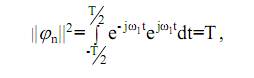
тогда коэффициенты ряда согласно (24) и принятым выше обозначениям определяется как

Учитывая, что 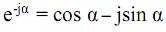, преобразуем (29)

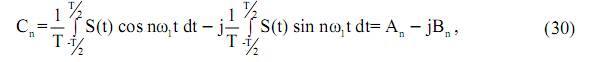
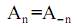– чётные, 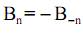– нечётные по индексу n составляющие. Это обстоятельство необходимо использовать при анализе произвольного колебания. Очевидно, что (30) можно представить в виде

Где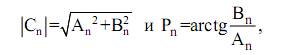

тогда ряд Фурье может быть записан в комплексной

и тригонометрической формах

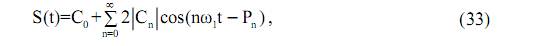
При этом в (33) считается, 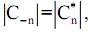в результате чего появляется удвоение. Поясним это на векторной диаграмме (рис. 24), принимая во внимание, что

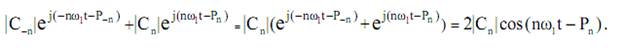
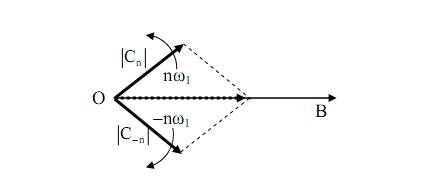
Рис. 24. К пояснению удвоения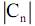

На оси ОВ отображаются проекции векторов 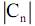, вращающихся в противоположные стороны. Используются также следующие формы записи ряда Фурье

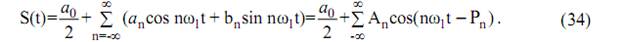
Сравнивая (33) и (34), нетрудно заметить, что

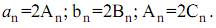
Здесь n – номер гармоники, под которой будем понимать отдельное гармоническое

колебание с частотой nω₁. Если n = 1, то гармоника называется основной (первой) (период сложного колебания совпадает с периодом ). Гармоники с частотами выше

ω₁, когда n > 1, называются высшими.

Поскольку представление временных зависимостей гармоник на одном графике делает его запутанным и нагроможденным, то совокупность амплитуд с частотами

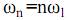изображают на частотной оси. Она является дискретной (линейчатой) и называется амплитудным спектром (АС). АС может изображаться в двухстороннем (рис. 25, а) и одностороннем (рис. 25, б) видах.

Рис. 25. Спектральная характеристика колебания

Зависимость начальных фаз гармоник от частоты носит название фазовым спектром (ФС) (рис. 25,в).

Рассмотрим пример. Пусть задано колебание прямоугольной формы с известной ампли-

тудой А и периодом Т₀ (рис. 26, а). Необходимо представить это колебание в виде ряда Фурье и привести его АС и ФС. Приведенная функция определяется во времени как

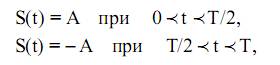
и является нечетной. Это означает, что A _n = 0 и

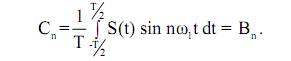
Определим эти коэффициенты ряда

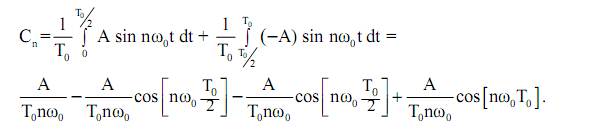
Принимая во внимание, 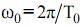, можно окончательно записать

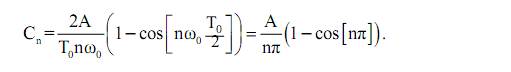
Из последнего выражения видно, что коэффициенты обнуляются при четных n и равны

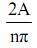при n = 1, 3, 5, 7.... Тогда ряд Фурье может быть записан, согласно (33) в виде

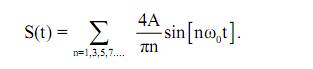
Проанализируем данный ряд. При n =1 амплитудное значение коэффициента ряда равно

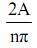, а частота 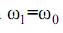(рис. 26, б).

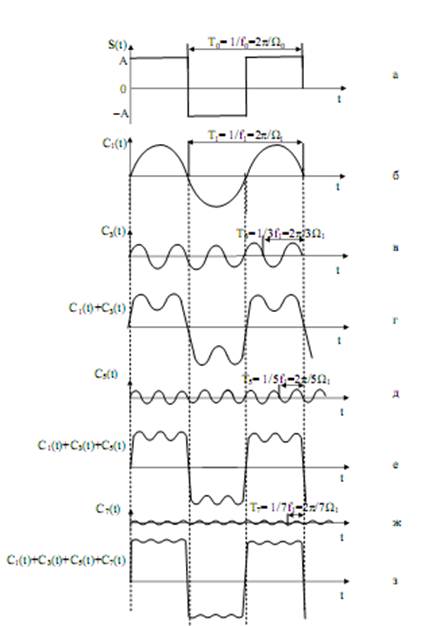
Рис. 26. Разложение колебания

Когда n=3, что соответствует третьей гармонике, амплитуда составляющей уменьшается в три раза (рис. 26, в). При суммировании первой и третьей гармоник результирующее колебание принимает вид, приведенный на рис. 26, г. Если к полученной сумме гармоник прибавить пятую (рис. 26, д), то результат приблизится к оригиналу заданной функции (рис. 26, е). Еще большее приближение к оригиналу можно получить при сложении полученного результата с седьмой гармоникой (рис. 26, ж), что иллюстрируется на рис. 26, з.

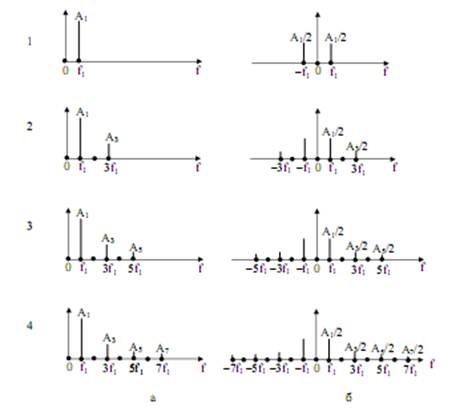
Рис. 27. Спектры гармоник:

а – тригонометрический; б – комплексный;

1 – первой; 2 – суммы первой и третьей; 3 – суммы первой, третьей

и пятой; 4 – суммы первой, третьей, пятой и седьмой

На рис. 27 приведена динамика трансформации спектра результирующего колебания

при росте числа гармоник в тригонометрическом и комплексном видах.

Приведенный пример позволяет сделать следующие выводы:

1) увеличение числа гармоник приводит к более точному описанию (восстановлению) колебания;

2) при росте номера гармоники ее амплитуда уменьшается;

3) начальная фаза гармоники существенно влияет на результат сложения.

Дата добавления: 2014-01-07