Формирование частотных характеристик замкнутой системы

Выше мы обсудили формирование частотных характеристик разомкнутой системы, соответствующих передаточной функции разомкнутой системы (косвенный метод проектирования). В этом разделе мы рассмотрим формирование частотных характеристик замкнутой системы (см. рис. ниже), соответствующих функции чувствительности и дополнительной функции чувствительности, с помощью выбора регулятора W₂(p) (прямой метод проектирования).

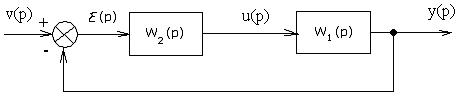
Как мы уже ранее показали, функция чувствительности S(p) является хорошим индикатором свойств замкнутой системы управления. Главное ее достоинство состоит в том, что если мы хотим, чтобы она принимала малые значения, то достаточно ограничиться рассмотрением ее модуля | S(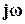)|; нет необходимости беспокоиться об ее фазе.

Постановка задачи. Типичные требования к качеству системы в рамках S включают в себя:

1. Минимально допустимая полоса пропускания ;

2. Максимально допустимая установившаяся ошибка или порядок астатизма;

3. Вид (форма) | S(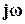)| в выбранной полосе частот;

4. Максимальное значение модуля S, | S()|.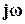

Последнее требование предотвращает усиление шума на высоких частотах и вводит запасы робастности. Как правило, выбирают 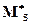= 2.

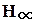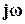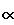
Условие 4 можно записать с помощью (H-бесконечность) нормы как || S()||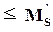. Кстати, 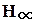норма (бесконечная форма) ПФ W(p) определяется как

|| W(p)||=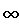

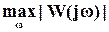
( см.рисунок ниже ). Здесь |c| означает абсолютное значение комплексного числа c.

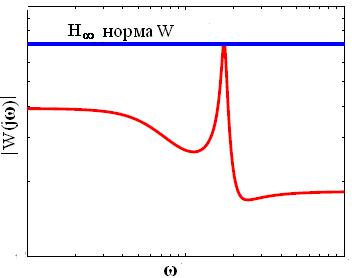
Все эти четыре требования можно аккумулировать (охватить) с помощью определения верхней границы 1/G_s(p) для модуля S, где G_s(p) функция веса, определяемая проектировщиком системы, и как результат все требования записать в виде одного требования

| S(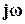)| (1)

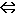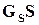|| ||< 1. (2)

Последнее условие вытекает из определения 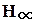нормы и словами его можно выразить следующим образом:

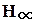норма взвешенной функции чувствительности |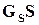| должна быть меньше, чем единица.

Рассматриваемая задача является разновидностью задачи 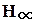- оптимального управления, которое заключается в том, чтобы найти оптимальный регулятор W₂(p), минимизирующий величину

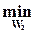|| G_s S(W₂ )|| <1. (3)

В выражении (3) sup есть символ операции supremum, которая означает, что конечный результат есть наибольшая верхняя граница.

На рис. 1 как пример показано, что чувствительность | S(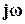)| на некоторых частотах превышает верхнюю границу 1/G_s(p). Поэтому полученная в результате взвешенная функция чувствительности больше единицы на тех же частотах, как видно на рис. 2.

Рис. 1

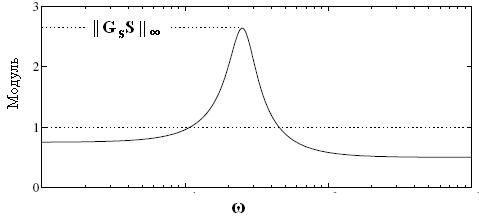
Рис. 2

Заметим, что обычно не используют логарифмический масштаб для модуля, когда изображают график взвешенной передаточной функции такой, как ||.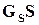

Выбор функций веса. Асимптотическая и точная логарифмические частотные характеристики типичной верхней границы 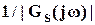представлены на рис. 3. Передаточная функция, соответствующая функции веса 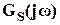обычно может быть представлена как

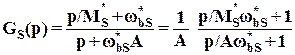
и мы видим, что 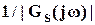(верхняя граница | S()|) равна A (типично малая величина ) на низких частотах и равна 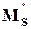> 1 на высоких частотах, и асимптота пересекает 1 на частоте , примерно равной требуемой полосе пропускания.

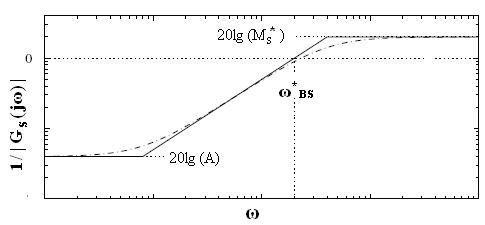
Рис. 3

Такой выбор функции веса определяет запретную область для функции чувствительности проектируемой системы (рис. 4).

Рис. 4

Замечание. Уменьшение функции чувствительности понижает влияние возмущающего воздействия и повышает точность воспроизведения задающего воздействия за счет увеличения полосы пропускания.

Смешанная чувствительность. Требование ||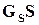 ||< 1 определяет нижнюю границу полосы пропускания 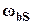, но никак не верхнюю ,

(см. рис. ниже)

и такое требование не дает нам возможность установить желаемый наклон ЛАЧХ разомкнутой системы L()=20lg|W(j)| за пределами полосы пропускания 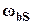. Чтобы сделать это, нам потребуется другая ПФ замкнутой системы, а именно, дополнительная функция чувствительности

T=1-S=W₁(p)W₂(p)S(p).

Например, можно установить верхнюю границу 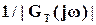модуля |T(j)|, и тем самым обеспечить требуемое значение максимума дополнительной функции чувствительности, другими словами, показателя колебательности M системы (обычно рекомендуемое значение M=1.25), и обеспечить достаточно быстрый спад L() на высоких частотах (рис. 5)

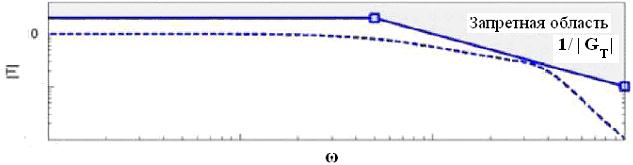
Рис. 5

Замечание. Уменьшение дополнительнлй функции чувствительности уменьшает влияние шума измерения и повышает робастность системы к мультипликативной неопределенности (см. ниже).

Также можно ограничить модуль управления

u(p)= W₂(p)S(p)[v(p)-W₁(p)f(p)]

( другими словами,ограничить функцию чувствительности управления W₂(p)S(p)) с помощью установления верхней границы для |W₂(p)S(p)| ( рис. 6), где

.

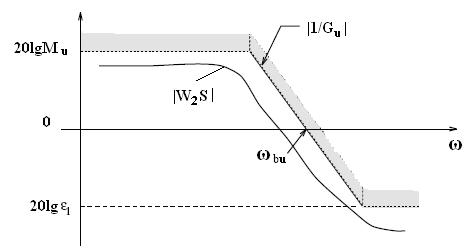
Рис. 6

Замечание. Уменьшение функции чувствительности управления уменьшает влияние шума измерения на управляющее воздействие, обеспечивает робастность системы к аддитивной неопределенности (см.ниже) и влечет умеренные значения АЧХ управляющего устройства.

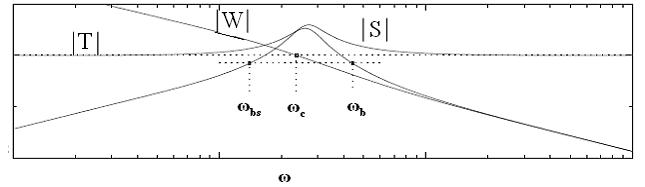
Смешанная чувствительность. В силу фундаментального ограничения

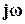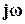S()+T()=1

Дата добавления: 2014-01-07