Опустить

SиTне могут одновременно быть малыми в одной и той же области частот. Поэтому любой метод проектирования, опирающийся на функции чувствительности, должен иметь возможность рассматриватьпару(S, T) (альтернативно пару(S, W2S))в отношении решения вопроса о том, на каких частотах должны быть или S, илиT (альтернативноSилиW2S)сделаны малыми. Такие методы совместно называют методами смешанной чувствительности.

При использованииоптимального 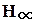- управления, чтобы объединить все рассмотренные выше требования в «смешанную чувствительность», применяют «пакетный метод», в результате получают следующее глобальное требование:

|| N||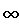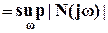<1; .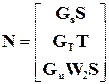

N естьвектор и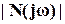представляет собой обычную евклидову норму

.

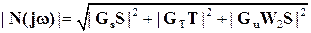После выбора вида N находим оптимальный регулятор W₂ (p) путем решения задачи минимизации

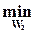|| N(W₂ )||.

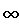Пример. Синтез с помощью смешанной чувствительности.

Рассмотрим ОУ, описываемый ПФ

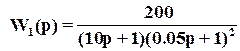
и для синтеза создадим смешанную чувствительность

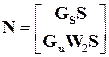
Пусть =1 и выберем фукцию веса для чувствительности

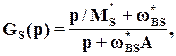
где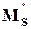 =1.5, 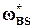=10, A=10^-4 . Значение 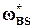=10 выбрано для того, чтобы получить значение частоты среза 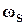, примерно равное 10 с^-1. 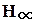проблему синтеза решаем с помощью Robust Control Toolbox в Matlab, используя процедуру mixsyn (W₁, G_S,G_u, []). В результате получаем регулятор с ПФ

.

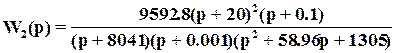Для данной задачи мы достигли оптимальной 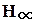нормы 1.31, так что требование к взвешенной чувствительности выполнено не полностью (см. рис. 6, на котором кривая | S(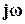)| проходит немного выше 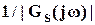). Между тем синтез можно считать успешным, т.к. || S||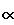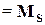=1.3, || T||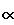=1, запасы устойчивости 1/h=8, 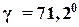и частота среза 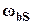= 7.22 с^-1, и переходная характеристика выглядит весьма удовлетворительно (рис. 7).

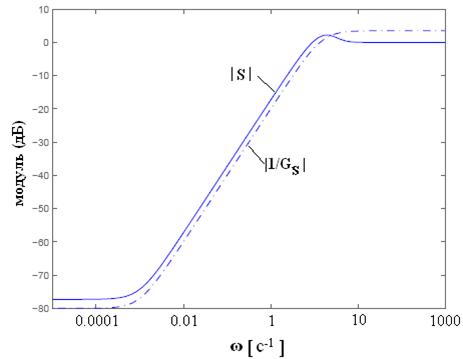
Рис. 6

Рис. 7

Дата добавления: 2014-01-07