H2 - и - оптимальное управление

Другой подход к проектированию САУ, опирающийся на понятие функции чувствительности, связан с нормализацией входных воздействий. Некоторые сведения о возможных входных воздействиях на систему являются важными, чтобы сформировать замкнутую систему надлежащим образом. Подход, рассмотренный ниже, связан с описанием входов, которые ограничены по норме. Следующий шаг- установить (определить) критерий качества системы путем ограничения приемлемой нормы выходного сигнала, в качестве которого часто выступает ошибка управления или отфильтрованная версия ошибки.

Нормализация входных воздействий. Выберем в качестве основного внешнего воздействия задающее воздействие v(t). В принципе можно выбрать и другое внешнее воздействие, например возмущающее воздействие. Задающее воздействие будем рассматривать как реакцию некоего фильтра с ПФ W_ф(p)=G_s (p), называемой в дальнейшем весом входа, на нормализованный в математическом смысле ограниченный вход v^’ (t), как показано на рис. ниже.

Преобразования Лапласа v(p) и v’(p) соответственно сигналов v(t) и v^’(t) связаны между собой соотношением

. (1)

Примем в качестве входа сигнал с v’(p)=1,так что для конкретного сигнала (задающего воздействия)

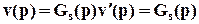. (2)

Например, если v(p)=1/p, то 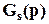= 1/p.

Класс (множество) ограниченных по 2 норме задающих воздействий (входных сигналов) можно представить как

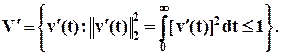. (3)

Левая часть выражения (3) называется «квадратом 2-нормы (второй нормы) входного сигнала v^’(t)». Нормы есть математические меры (критерии), которые позволяют сравнивать между собой элементы одного и того же множества. Путем фильтрации v^’(t) мы определяем новый класс сигналов

Используя теорему Парсеваля, выражение (3) можно вычислить в частотной области с помощью

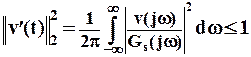. (4)

Замечание. Для того чтобы можно было построить физически осуществимое управляющее устройство, все сигналы, поступающие на систему, должны быть ограниченными.

Предположим теперь, что сигнал

( 5 )

представляет гармонический (синусоидальный сигнал) с неизвестной частотой и неизвестной зависящей от частоты и ограниченной единичным значением амплитудой ,

. (6)

Согласно (1) и исходя из физического смысла АФХ фильтра, получаем

,

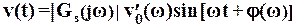где фаза гармонического сигнала v(t):

,

или

, (7)

причем амплитуда гармонического сигнала v(t):

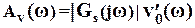. (8)

Модель (7) описывает множество задающих воздействий (сигналов) с неизвестной ограниченной амплитудой 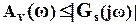. Такое множество содержит синусоиды с апплитудами, зависящими от частоты. Значение можно трактовать как верхнюю границу возможной амплитуды сигнала с конкретной частотой 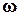. Фаза 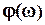каждого сигнала, входящего в множество, также зависит от частоты, и ее можно считать в рамках бесконечной нормы (см. ниже) также неизвестной величиной.

Линейное квадратичное H₂ - оптимальное управление. Интегральный критерий качества, когда не накладывается никаких ограничений на управление, имеет вид

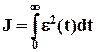. (9)

Задача H₂ – оптимального управления состоит в том, чтобы найти управляющее устройство с ПФ W₂ (p), которое для конкретного задающего воздействия v(t) минимизирует квадрат 2-нормы ошибки , записываемой как . Преобразование Лапласа ошибки в отсутствие возмущающего воздействия и шума измерений можно записать с помощью функции чувствительности 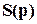в виде

. (10)

Для кокретного задающего воздействия из выражения (2) имеем

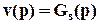. (11)

Используя теорему Парсеваля с учетом (9) задачу H₂ – оптимального управления можно сформулировать в частотной области как

. (12)

Подставляя (10) и (11) в (12), получаем

. (13)

Следовательно, H₂ – оптимальное управление минимизирует среднее значение взвешенной функции чувствительности с весом 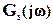, где 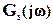зависит от конкретного выбранного задающего воздействия 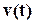. В математическом смысле H₂ - управляющее устройство мимнимизирует «2 -норму функции чувствительности, взвешенной с помощью .

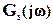- оптимальное управление. В задаче - оптимального управления предполагается, что все задающие воздействия принадлежат множеству ограниченных по норме с весом 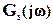функций, как определено выражением (7). Каждому конкретному задающему воздействию v(t) из этого множества независимо от фазы будет соответствовать согласно (8) и (10) свое значение ошибки с амплитудой

.

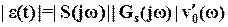Наибольшая возможная ошибка для конкретной частоты

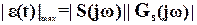
будет иметь место, когда =1.

- оптимальное управляющее устройство проектируется так, минимизировать возможную максимальную ошибку, другими словами, бесконечную норму ошибки

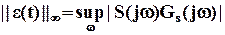, (14)

которая (ошибка) может появиться от любого задающего воздействия, входящего во множество допустимых входов (7). В выражении (14) sup есть символ операции supremum, которая означает, что конечный результат есть наибольшая верхняя граница Задача - оптимального управления может быть формально представлена как

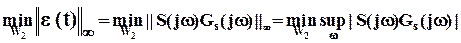. (15)

. Следовательно, - оптимальное управляющее устройство минимизирует максимальное значение взвешенной функции чувствительности в диапазоне частот 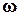от нуля до бесконечности или в математическом сысле минимизирует 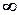-норму функции чувствительности с весом .

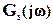Путем соответствующего взвешивания с помощью 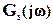можно сформулировать условие - качества в виде

,

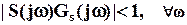или

.

Как это можно сделать, было показано ранее в лекции, связанной с формированием частотных характеристик замкнутой системы.

Стратегия оптимального управления соответствует поступкам человека в неопределенной ситуации. Надо исходить из возможной наихудшей ситуации и затем планировать свои действия так, чтобы выйти из нее с наименьшими потерями.

Преимущества применения нормы для формулировки требований качества в сравнении с заключаются в следующем:

1. Проектировщик может ограничить максимальное значение 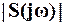прямо путем соответствующего выбора функции веса .

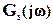2. Также используя функцию веса 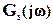, проектировщик может установить полосу пропускания функции чувствительности 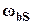, определяемую как частоту, начиная с которой 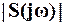становится меньше 0.707 (-3дБ).

Кроме того, норма дает в руки проектировщика инструмент для формулировки робастного качества. Мы на этом остановимся в следующем разделе.

Дата добавления: 2014-01-07