Лекция 32

Синтез управляющего устройства с помощью Q – параметризации (Q – синтез)

Формулы (3) и (4) положены в основу продвинутого метода синтеза систем управления, так называемого Q - синтеза. Основная идея этого метода: найти УУ Q(p) с помощью (4) и затем получить ПФ классического УУ, используя (3), и тем самым перейти к классической структуре системы с единичной обратной связью.

Преимущество такого метода заключается в том, что ПФ классической системы с обратной связью

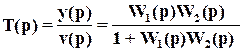
нелинейна относительно ПФ УУ (регулятора) 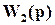, что затрудняет поиск 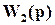для достижения желаемых свойств замкнутой системы. При условии 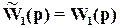ПФ для системы с внутренней моделью

T(p)=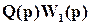

линейна в отношении УУ Q(p) (или, как говорят, T(p) аффинна в Q(p)), чтопозволяет для простых моделей решить задачу синтеза ручным путем. При этом устойчивость замкнутой системы гарантирована, если устойчиво УУ Q(p) и 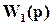, т.е. соотношение (3) известно, как параметризация всех регуляторов, обеспечивающих устойчивость замкнутой системы, в случае устойчивых объектов. Ключевой момент параметризации (3), что она описывает все возможные УУ (регуляторы), обеспечивающие устойчивость замкнутой системы для данного объекта .

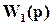Кстати, функция чувствительности также афинна в Q(p),

S(p)=1 - Q(p)W₁ (p).

При этом передаточная функции по возмущению и передаточная функция, связывающая управление и шум измерения оказываются соответственно равными

Все ПФ T(p), 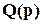, , 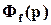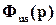являются устойчивыми, если устойчивы объект управления 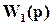и УУ Q(p). При этом гарантирована внутренняя устойчивость системе управления, и регулятор с ПФ

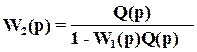
стабилизирует систему.

Следовательно, Q –параметризация или аффинная параметризация в общем случае облегчает решение задачи синтеза системы управления, в частности получения робастной системы.

Однако по нескольким причинам невозможно найти инверсию (4) даже в том случае, когда модель ОУ является точной.

а) ОУ является устойчивым и минимально-фазовым

Если 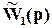является строго физически осуществимой, то инверсия имеет больше нулей, чем полюсов, т.е. физически неосуществима. Альтернативно можно выбрать

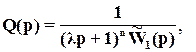(5)

где n выбирается достаточно большим так, чтобы сделать ПФ Q(p) физически осуществимой. Параметр 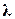влияет на быстродействие системы.

Пример. Модель объекта первого порядка

Пусть

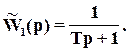
Выбираем n =1. При этом

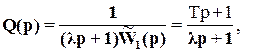
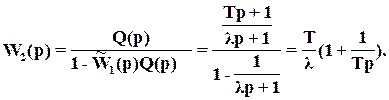
Как видим, получаем ПИ-регулятор.

б) ОУ является устойчивым и неминимально-фазовым

Если ОУ является неминимально- фазовым имеет неустойчивые нули (правые нули), то его инверсия Q(p) будет неустойчивой. Альтернативно можно удалить неустойчивый множитель (-(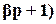(ему соответствует неустойчивый нуль z=1/ 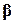) из числителя ПФ модели ОУ или заменить его на множитель (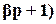. В последнем случае изменяется только фазо-частотная характеристика псевдообъекта, а его АЧХ не отличается от модели объекта.

Пример.

Пусть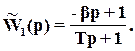

При этом

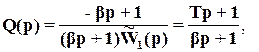
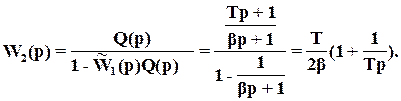
Как видим, получаем ПИ-регулятор.

в) ОУ содержит чистое запаздывание

В этом случае реализовать инверсию оказывается невозможным, т.к. она должна предсказывать будущие значения входа, должна быть идеальным предсказателем. Альтернативно можно удалить запаздывание перед инвертированием. Другой подход приводит к предиктору Смита.

Рассмотрим модель ОУ

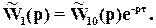
Пусть 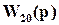=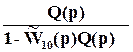будет УУ, которое мы используем без учета запаздывания. Тогда

. (6)

Эмпирическое правило говорит нам о том, что именно это Q(p) нам следует использовать также для объекта с запаздыванием. При этом получаем

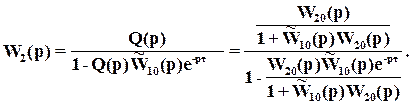
Эта модификация 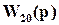с учетом запаздывания известна как компенсация чистого запаздывания (рис. 3), впервые полученная Отто Смитом. Дело в том, что при 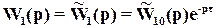, ПФ замкнутой системы

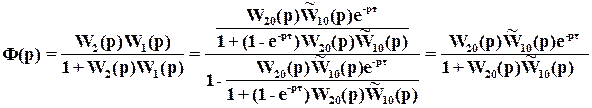
не содержит звена чистого запаздывания 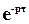в знаменателе.

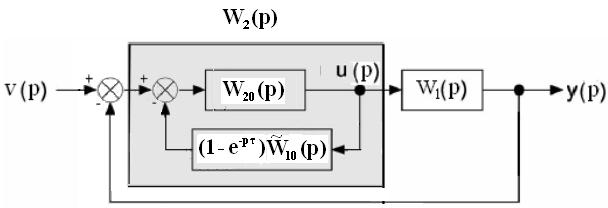
Рис. 3

На рис. 4 изображена структурная эквивалентная схема системы управления с обратной связью, где Q(p) определяется по (6). Что дает предиктор Смита? При

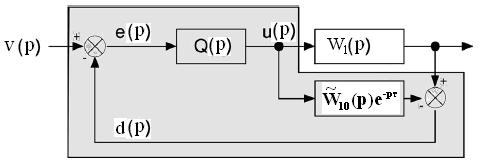
Рис.4

одном и том же перерегулировании длительность переходного процесса значительно сокращается (жирные линии) по сравнению со стандартным ПИ-регулятором (тонкие линии), включенном вместо W₂ (p) (рис. 4).

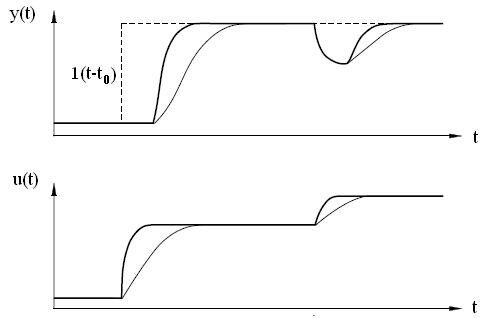
Рис. 4

Дата добавления: 2014-01-07