Определение дифференциального уравнения. Основные понятия

Однородные дифференциальные уравнения первого порядка.

Линейные дифференциальные уравнения первого порядка.

Дифференциальные уравнения первого порядка с разделяющимися переменными.

Дифференциальные уравнения первого порядка. Основные понятия. Теорема существования и единственности решения.

Определение дифференциального уравнения. Основные понятия.

Лекция 13. Дифференциальные уравнения первого порядка.

Определение. Уравнение, связывающее независимую переменную x с

неизвестной функцией и ее производными до некоторого порядка n включительно, называется дифференциальным уравнением 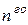порядка.

Общий вид дифференциального уравнения 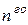порядка: .

Определение. Решением дифференциального уравнения называется функция , имеющая производные до 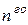порядка включительно и такая, что ее подстановка в уравнение обращает его в тождество.

Определение. Функция, являющаяся решением дифференциального уравнения и зависящая от произвольных постоянных, число которых равно порядку дифференциального уравнения называется общим решением дифференциального уравнения.

Например, для уравнения 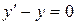функция 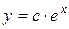является общим решением.

Определение. Решение дифференциального уравнения, полученное из общего, путем придания конкретных значений постоянным, входящим в общее решение, называется частным решением.

Процесс нахождения решения дифференциального уравнения принято называть интегрированием этого уравнения, график решения - интегральной кривой данного уравнения.

Дата добавления: 2014-01-07