Мощность множества

Когда речь идет о конечном множестве, одной из его характеристик является число элементов этого множества. Как же с подобной точки зрения характеризовать множества, содержащие бесконечные наборы элементов? Естественным для такой характеристики является сравнение бесконечных множеств между собой или с каким-то бесконечным «эталонным» множеством. Множества считаются равномощными, если существует взаимно однозначное соответствие между всеми элементами одного и другого множеств. Это означает, что существует закон, в соответствии с которым каждому элементу одного множества соответствует единственный элемент второго множества, причем разным элементам первого множества соответствуют разные элементы второго множества и все элементы второго множества имеют прообразы в первом множестве.

Примером задания взаимно однозначного соответствия между множествами точек двух отрезков является гомотетия:

Таким образом, «количество» точек верхнего и нижнего отрезков вследствие взаимно однозначного соответствия между точками одинаково, хотя один отрезок длиннее другого. Все дело в том, что точки, как известно, не имеют длины, и присутствие или отсутствие на отрезке отдельных точек не связано с изменением этой меры отрезка.

Взаимно однозначное соответствие между множествами на вещественной оси можно задавать с помощью функций. Так, функция (что в данном случае равносильно 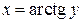) задает взаимно однозначное соответствие между точками интервала и точками всей вещественной оси. Таким образом, множество точек любого интервала равно множеству точек всей вещественной прямой.

В математике очень важным является понятие счетного множества. Счетным называется множество, равномощное множеству натуральных чисел 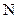. Примером счетного множества является множество целых чисел. Действительно, хотя 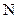является подмножеством , между точками этих множеств можно установить взаимно однозначное соответствие с помощью следующего правила. Присвоим числу 0 номер 1, числу 1 – номер 2, числу -1 – номер 3, числу 2 – номер 4, числу -2 – номер 5…. Таким образом, целому положительному числу n поставим в соответствие натуральное число 2n; отрицательному целому числу - n поставим в соответствие натуральное число 2n+1. Взаимно однозначное отображение установлено, следовательно, счетно.

Множество рациональных чисел также является счетным. «Сосчитать» его, то есть, установить взаимно однозначное соответствие с множеством 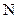можно при помощи следующей бесконечной таблицы.

В верхней строке таблицы стоят целые числа (p), начиная с 0. В левом крайнем столбце – натуральные числа (q). На пересечении строки и столбца стоит рациональное число p/q.

q\p			-1		-2		-3		…….
			-1		-2		-3		……
		1/2	-1/2		-1	3/2	-3/2		……
		1/3	-1/3	2/3	-2/3		-1	4/3	……
		1/4	-1/4	1/2	-1/2	3/4	-3/4		……
		1/5	-1/5	2/5	-2/5	3/5	-3/5	4/5	……
….	…….	…	….	…	…	…	….	…	……

Очевидно, что некоторые числа в таблице повторяются. Но для любого рационального числа найдется место в таблице на пересечении столбца, соответствующего числителю, и строки, соответствующей знаменателю. Начнем двигаться по таблице с левой верхней позиции по такому пути, чтобы пройти все элементы таблицы. Можно, например, двигаться по следующему маршруту.

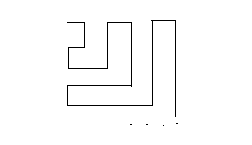
При этом попадающиеся по пути рациональные числа последовательно нумеруются и запоминаются, так как номера присваиваются только еще не пронумерованным числам. При указанном способе движения числу 0 присваивается номер 1, числу 1 – номер 2, числу 1/2 – номер 3, числу 1/3 – номер 4, числу -1/3 – номер 5, …..Указанная процедура (бесконечная) обеспечит нумерацию всех рациональных чисел, причем ни одно не будет пронумеровано дважды. Взаимно однозначное соответствие установлено.

Возникает вопрос: можно ли пронумеровать все вещественные числа? Ответ на этот вопрос отрицательный. Покажем, что множество точек любого интервала, лежащего на вещественной оси, несчетно. Поскольку между точками двух интервалов можно установить взаимно однозначное соответствие, докажем несчетность множества точек интервала (0,1). Доказательство проведем методом «от противного».

Заметим, что в силу взаимно однозначного соответствия любую точку на интервале (0,1) можно ассоциировать с десятичной дробью вида 0,…….., где после нуля и запятой стоит бесконечное множество цифр, принимающих значения от 0 до 9. В случае, когда десятичная дробь конечная, все цифры, начиная с некоторой, будут нулями. Предположим, что мы смогли присвоить номера всем точкам интервала или, что то же самое, всем десятичным дробям указанного вида. Следовательно, мы можем расположить все такие числа последовательно, в соответствии с нумерацией:

1)

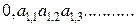
2)

3)

………………………

n)

……………………..

Здесь все , 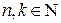– цифры, принимающие значения 0,1,2,3,4,5,6,7,8 и 9.

А теперь построим новую десятичную дробь с нулем в целой части: 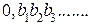., где 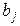– также цифры из множества {0,1,2,3,4,5,6,7,8,9}. При построении выберем цифру 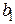так, чтобы , цифру так, чтобы 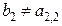,………., ,………. У нас получится новая точка из интервала (0,1), не совпадающая ни с одной точкой из пересчитанных, так как соответствующая новой точке десятичная дробь отличается от каждой из пересчитанных десятичных дробей хотя бы одной цифрой после запятой. Таким образом, мы пришли к противоречию, предполагая, что можем пересчитать все точки: мы нашли точку из интервала (0,1), не совпадающую с пересчитанными точками.

Мощность множества точек интервала (0,1), а значит, в силу равномощности, и мощность множества всех вещественных чисел называется континуум. В 1878 году Г.Кантор выдвинул гипотезу о том, что любое бесконечное подмножество множества вещественных чисел либо счетно, либо имеет мощность континуум. До сих пор эта гипотеза не доказана и не опровергнута.

Дата добавления: 2014-01-07