Теорема Вейерштрасса

Пусть является бесконечным ограниченным множеством. Тогда 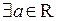тчо – предельная точка множества A.

Доказательство. Раз множество A ограничено, то , где 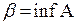, 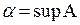. Если точка 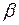является предельной точкой множества A, то теорема доказана. Предположим, что 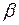не является предельной для множества A, то есть, . Значит, в проколотой окрестности точки 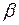нет точек множества A. В таком случае 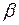, являясь точной нижней гранью, необходимо должна принадлежать множеству A, значит, 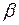является дискретной точкой множества A.

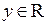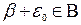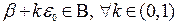Рассмотрим новое множество B таких точек , для которых на бесконечном интервале находится конечное число точек множества A. Согласно нашему предположению на бесконечном интервале находится одна точка , следовательно, и . Множество B ограничено сверху, потому что 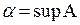является мажорантой для B, так как на бесконечном интервале 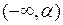находится все бесконечное множество A. Следовательно, .

Для 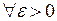бесконечный интервал содержит либо конечное множество точек множества A, либо вообще не содержит точек множества A. Так как , бесконечный интервал 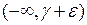содержит уже бесконечное множество точек множества A. Следовательно, 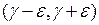содержит бесконечное множество точек множества A. Поэтому 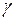является предельной точкой множества A. Теорема доказана.

Способы задания функций

Определение 1. Если каждому элементу некоторого множества ставится в соответствие элемент множества 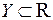, говорят, что на множестве 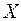задана функция , здесь 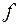определяет закон, с помощью которого осуществляется это соответствие.

Примеры. 1. Показательная функция

2. Логарифмическая функция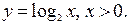

3. Степенная функция .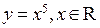

Функция может быть задана в виде таблицы или графика, либо формулой (аналитическое задание). В качестве примера приведена функция, аналитическое задание которой , а табличное и графическое ее задания приведены ниже.

x		1.5		2.5
y		2.25		6.25

Аналитически функцию можно задать в явном виде 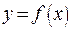(явное задание функции), когда из формулы следует, что переменная зависит от , то есть является функцией аргумента .

Можно задать ее неявно , когда любая из переменных может считаться независимой, тогда другая переменная является функцией. Пример неявного задания функции . Нетрудно заметить, что эта формула задает фактически две непрерывные функции

и 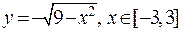. График первой функции представляет верхнюю полуокружность, график второй – нижнюю ее часть. Если не требовать непрерывности, то из соотношения можно получить бесчисленное множество функций, заданных на отрезке [-3,3].

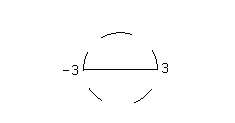
Кроме того, возможно параметрическое задание функции 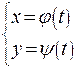, когда вводится дополнительный параметр . Примером является параметрическое уравнение той же, что и выше окружности 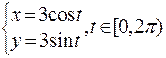, в неявном виде записанное как .

Определение 2. Множество 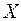называется областью существования функции, или областью ее определения.

Определение 3. Множество называется областью значений функции.

Числовые последовательности.

Числовой последовательностью называют счетный набор пронумерованных чисел . Последовательность также можно рассматривать как функцию, заданную на множестве N. Число 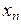называют членом последовательности, – номером этого члена последовательности.

Примеры. 1) , 2), 3), 4) .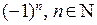

Легко заметить, что члены первой и третьей последовательностей с ростом приближаются к конкретной величине, члены второй последовательности безгранично увеличиваются, а члены четвертой последовательности поочередно принимают два значения.

Введем определение предела последовательности, используя кванторы общности и существования для отображения динамики процесса.

Определение. Число называется пределом последовательности , (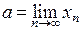), если для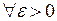 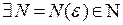такое, что при справедливо неравенство: .

Пример. Покажем, что . Здесь 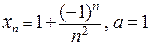. Так как , найдем такое значение , что при (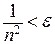). Так как последнее неравенство эквивалентно неравенству 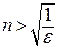, за можно принять наибольшее целое число, меньшее или равное 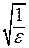. Такое число обозначается как [].

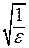Дата добавления: 2014-01-07