Принцип Архимеда и его следствия

Принцип Архимеда. Пусть 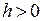– фиксированное число. Тогда для тчо .

Доказательство. Рассмотрим множество . Множество A ограничено снизу, следовательно согласно Утверждению 1-а 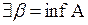. В соответствии с Утверждением 2-а при 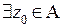тчо 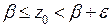. В полуинтервале 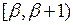может лежать только одно целое число. В силу того, что 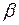– точная нижняя грань подмножества A целых чисел, 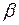совпадает с целым числом 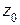и является минимальным элементом множества A. Следовательно, , то есть, . Так как 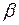– минимальный элемент множества A, . То есть . Таким образом, является искомым целым числом.

Следствие 1. 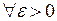тчо .

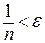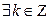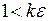Доказательство. Применим принцип Архимеда для и . тчо . Из правой части двойного неравенства следует: и 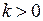. Таким образом, целое число является натуральным числом, 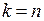. И мы получили требуемое неравенство .

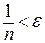Следствие 2. Для , , 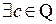тчо .

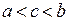Доказательство. В соответствии со Следствием 1 при 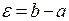найдем 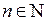тчо . В соответствии с Принципом Архимеда при и 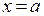найдем 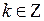тчо 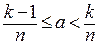. Имеем 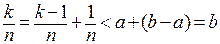. Следовательно, 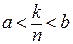. Рациональное число найдено.

Классификация точек подмножеств R

Окрестностью точки называют любой интервал тчо .

окрестностью точки называют интервал . Обозначают такую окрестность .

Проколотой окрестностью точки называют множество 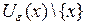. Обозначают проколотую окрестность .

Точка 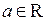называется предельной точкой множества , если . То есть, в любой окрестности точки находятся точки из множества A.

Примеры. Точка 0 является предельной для множества 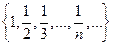, и не принадлежит этому множеству. Точка 0 является предельной для множества точек интервала (0,1) и также не принадлежит этому множеству. Точка 0 является предельной для множества точек полуинтервала [0,1) и принадлежит этому множеству.

Точка является дискретной точкой множества A, если или, что то же самое, . То есть дискретная точка множества такова, что существует ее окрестность, в которой нет других точек множества, кроме нее самой.

Пример. Множество 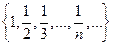состоит только из дискретных точек.

Точка является внутренней точкой множества A, если . То есть, внутренняя точка входит в множество с некоторой своей окрестностью.

Множество называется открытым, если состоит только из внутренних точек.

Примеры. Множество точек интервала (0,1) является открытым, в то время как множество точек полуинтервала [0,1) не является открытым: точка 0 не является внутренней точкой данного полуинтервала.

Множество называется замкнутым, если его дополнение до R, то есть, множество 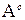, является открытым.

Пример. Множество точек отрезка [0,1] является замкнутым.

Утверждение. Множество замкнуто тогда и только тогда, когда оно содержит все свои предельные точки.

Необходимость. Пусть A замкнуто, то есть, пусть 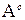– открытое множество. Докажем, что все предельные точки A принадлежат A методом от противного. Предположим, что – предельная точка множества A – такая, что 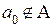. В таком случае . Поскольку 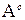– открытое множество, является внутренней точкой множества 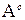, то есть, . Следовательно, , и значит, не может быть предельной точкой множества A.

Достаточность. Пусть множество A содержит все свои предельные точки. Покажем, что 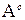– открытое множество, то есть, если 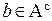, то 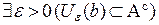. Предположим противное: пусть для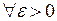 . Согласно определению точка – предельная точка множества A, и значит 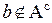. Мы пришли к противоречию.

Дата добавления: 2014-01-07