Примеры решения задач. 5.2.2. Пусть вероятность дожить до 20 лет равна p1, а вероятность дожить до 60 лет равна р2, (р2 < p1)

5.2.2. Пусть вероятность дожить до 20 лет равна p ₁, а вероятность дожить до 60 лет равна р ₂, (р ₂ < p ₁). Чему равна вероятность того, что человек, доживший до 20 лет, доживет до 60?

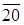Решение. Построим пространство элементарных исходов. Эксперимент заключается в выборе случайного человека и фиксировании длительности его жизни. Имеем всего три исхода: . Обозначение “” означает, что человек не дожил до 20 лет, обозначение “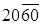” - что он дожил до 20 лет, но не дожил до 60, обозначение “60” означает, что человек дожил до 60 лет. Событие А = {человек дожил до 60 лет} влечет событие В = {человек дожил до 20 лет}. По условию р (А) = р ₂, р (В) = p ₁, тогда

.

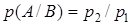5.2.4. Вероятность того, что стеклянный сосуд при упаковке будет разбит, равна 0,01. Определить вероятность того, что при упаковке пяти сосудов хотя бы один окажется разбитым.

Решение. В условии неявно подразумевается, что события { i- й сосуд окажется разбитым}, i = 1, 2, 3, 4, 5 независимы в совокупности. Поэтому вероятность события В = {хотя бы один сосуд окажется разбитым} равна

.

5.2.5. Вероятности двух несовместных событий А и В связаны соотношением 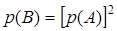; кроме того, А + В = W. Найти р (А) и р (В).

Решение. По условию , кроме того, в силу несовместности событий, . Подставив вместо числа р (В) квадрат числа р (А), получим квадратное уравнение , откуда .

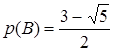5.2.6. Двадцать мальчиков поехали на пикник; 5 из них обгорели на солнце, 8 были сильно искусаны комарами, а 10 мальчиков остались всем довольны. Какова вероятность того, что обгоревший мальчик не был искусан комарами? Какова вероятность того, что искусанный комарами мальчик также и обгорел?

Решение. Введем обозначения: А = {наудачу выбранный мальчик обгорел}, В = {наудачу выбранный мальчик искусан комарами}. Тогда событие АВ означает, что выбранный мальчик обгорел и искусан комарами, а событие 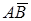означает, что мальчик обгорел и не искусан комарами. Непосредственно из условия задачи вытекает, что одновременно и обгоревших, и искусанных мальчиков было трое. Тогда обгоревших и неискусанных мальчиков было двое, откуда получаем, что, , .

Нужно найти условные вероятности и . Используя определение условной вероятности, получаем

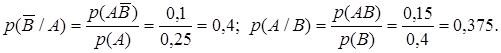
5.2.8. Из 12 билетов, пронумерованных от 1 до 12, один за другим выбираются без возвращения два билета. Каковы вероятности следующих событий: A = {оба номера на билетах четные}; В = {первый номер четный, второй нечетный}; С = {один номер четный, другой нечетный}.

Решение. Введем следующие обозначения событий:

Ч_k = { k- й выбранный билет имеет четный номер}; k = 1, 2.

Н_k = { k- й выбранный билет имеет нечетный номер}; k = 1, 2.

Тогда , , .

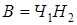Из условия задачи находятся следующие вероятности: ; ;

Нам нужно найти вероятности:

; =

= , а также вероятность .

События несовместны, поэтому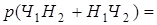

= = .

Замечание. Эту задачу можно решить по “классическим” канонам. Действительно, взять один за другим два билета – это то же самое, что взять два билета сразу. Поэтому вероятности событий А, В, С равны:

; ; .

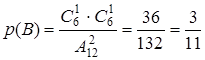5.2.10. Игральную кость подбрасывают до первого выпадения одного очка. Какова вероятность того, что придется произвести более трех подбрасываний?

Решение. Пространство W содержит в данном случае счетное бесконечное число исходов, W = {1, 2, …, k, …}, где элементарный исход k соответствует случаю, когда первые (k – 1) бросаний не привели к выпадению единицы, а результатом k- го бросания была единица. Обозначим через 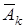событие {при k -м бросании единица не выпала }. В условии задачи подразумевается, что события 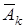, k = 1, 2, 3, … независимы в совокупности, а вероятности событий таковы:

Элементарный исход k можно представить в виде произведения

. Значит, . Отсюда ,

, .

Событию А = {придется произвести более трех бросаний кости} противоположно событие = { произведено не более трех бросаний}.

, , =

= 1.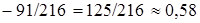

Дата добавления: 2014-01-07