Интегрирование выражений, рационально зависящих от функций

.

Приравнивая коэффициенты при одинаковых степенях в обеих частях этого равенства, получаем систему линейных уравнений:

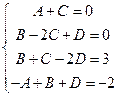. Отсюда следует, что 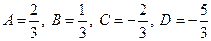. Поэтому

.

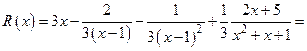
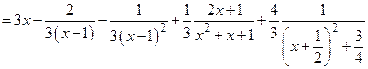Окончательно получаем .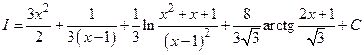

2. Вычислить неопределенный интеграл .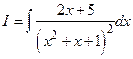

Снова 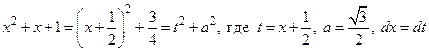. Поэтому

.

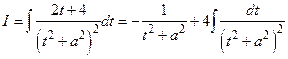Применяя ко второму слагаемому рекуррентную формулу при 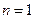, получаем

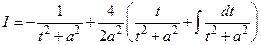
или

.

После упрощения получаем .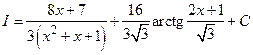

1˚. Интегралы вида 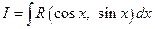, где 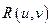− дробно-рациональная функция, приводятся к интегралам от рациональных дробей (рационализуются) при помощи так называемой универсальной тригонометрической подстановки 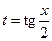. Действительно, в этом случае , , 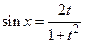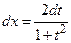. Поэтому

.

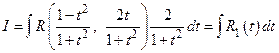2˚. В некоторых частных случаях бывает удобнее пользоваться менее универсальными, но более простыми подстановками для рационализации подынтегрального выражения.

§ Если 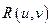зависит 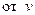нечетно, т.е. , где 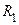− рациональная функция, целесообразно сделать замену 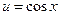, так как

.

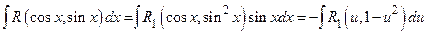§ Точно так же, если 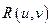нечетно зависит 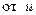, можно положить .

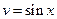§ Если функция 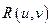четна относительно совокупности переменных, точнее, , то удобно воспользоваться замено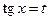й или .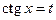

Пример 1.. Вычислитьинтеграл .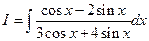

1-й способ. Полагая , приходим к интегралу от рациональной дроби: 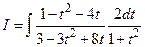. Попробуем применить более простую подстановку.

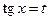2-й способ. Так как здесь, можно принять . Тогда получим 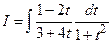. Это уже лучше!

3-й способ. Обозначим знаменатель 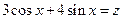и представим 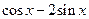в виде 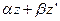. Так как 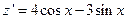, то будет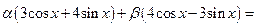 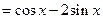, и мы приходим к системе уравнений: 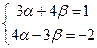, откуда следует, что 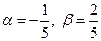. Поэтому .

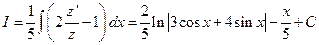Пример 2. Вычислить интеграл .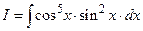

Так как 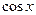входит в нечетной степени, то полагаем 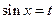, тогда будет 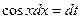и потому

=.

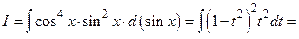
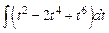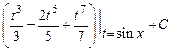Пример 3. Вычислить интеграл 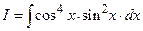. Здесь обе функци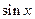и и 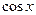входят в четных степенях. Придется понижать степень обеих этих функций.

=.

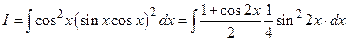
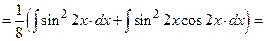
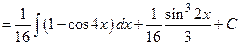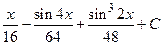Пример 4. Вычислить интеграл .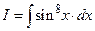

Формулы Эйлера дают:

.

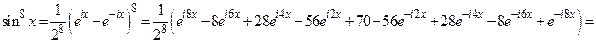
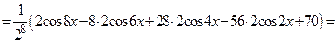
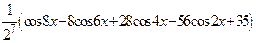Поэтому .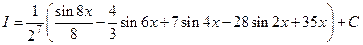

В теории рядов Фурье часто приходится вычислять интегралы вроде следующего.

Пример 5. Вычислить интеграл .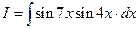

Имеем .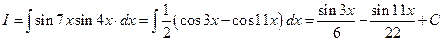

Дата добавления: 2014-01-07