
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способы определения порядка реакций
При определении порядка реакции для того, чтобы можно было использовать более простые решения кинетических уравнений, эксперимент удобно проводить при равных исходных концентрациях реагирующих веществ или при большом избытке всех реагентов, кроме одного. В этом случае по мере протекания реакции заметно изменяется концентрация только реагента, взятого в малом количестве. Концентрации остальных веществ практически остаются постоянными. Изучая изменение концентрации взятого в малом количестве вещества, можно определить порядок реакции по этому веществу. Затем такую же операцию проводят с каждым из остальных участников реакции. Общий порядок реакции равен сумме порядков по отдельным реагирующим веществам.
Рассмотрим наиболее частые способы определения порядка реакции.
1. Способ подстановки (когда использование одного из приведенных выше уравнений дает постоянную величину константы скорости, реакция имеет соответствующий порядок.)
2. Способ Оствальда – Нойеса
Способ основан на определении времени, в течение которого концентрация вещества уменьшается в определённое число раз ν. Из решения кинетического уравнения для скорости реакции n-го порядка для времени уменьшения концентрации в ν раз получается уравнение:
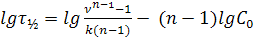 (15.12)
(15.12)
В координатах 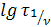 = f(lgC0) этому уравнению соответствует прямая, тангенс угла наклона которой равен 1− n.
= f(lgC0) этому уравнению соответствует прямая, тангенс угла наклона которой равен 1− n.
3. Графический метод: для реакции первого порядка характерна линейная зависимость lgC – t, второго порядка – линейная зависимость 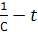 , третьего порядка – линейная зависимость
, третьего порядка – линейная зависимость 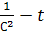 . В реакциях нулевого порядка скорость реакции постоянна во времени (гетерогенные процессы).
. В реакциях нулевого порядка скорость реакции постоянна во времени (гетерогенные процессы).
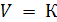
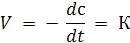
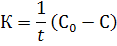
Размерность К − 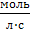 .
.
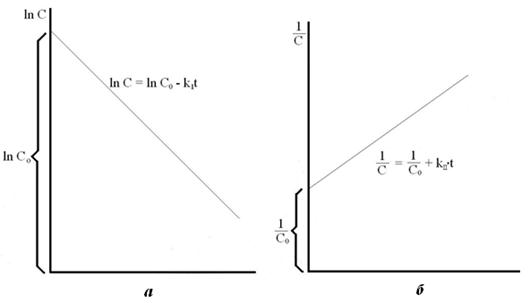
Рис. 15.1
а) Зависимость 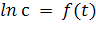 для реакций первого порядка;
для реакций первого порядка;
б) Зависимость 1/С= f(t) для реакций второго порядка.
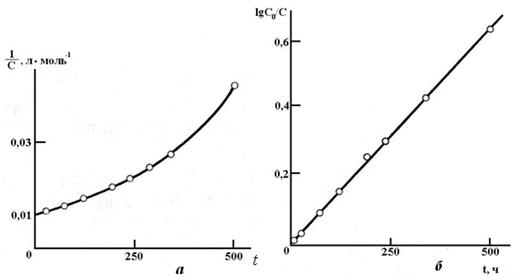
Рис. 15.2 Обработка экспериментальных результатов по инверсии сахарозы в координатах: а) 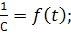 б)
б) 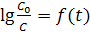 .
.
4. Способ определения периода полураспада τ½. Было показано, что для реакции первого порядка период полураспада τ½ не зависит от начальной концентрации, для реакции второго порядка τ½ обратно пропорциональна концентрации, а для реакции третьего порядка − обратно пропорциональна квадрату концентраций.
Кинетические уравнения реакций различных порядков и их решение
Таблица 15.1
| Порядок реакции | Уравнение скорости | Результаты интегрирования | Размерность константы скорости | Функция концентрации (с), линейно зависящая от времени | τ½ |
–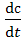 =k0 =k0
| с0–с=kot | 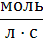
| с | 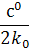
| |
–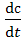 =kIc =kIc
| ln 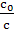 =k1t =k1t
| с–1 | ln c | 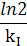
| |
–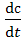 =kIIc2 =kIIc2
|  – –  =kIIt =kIIt
| 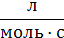
| 
| 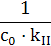
| |
–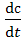 =kIIIc3 =kIIIc3
| 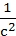 – – 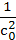 =2kIIIt =2kIIIt
| 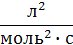
| 
| 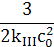
| |
| n | –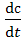 = kncn = kncn
| 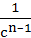 – – 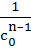 =(n–1)knt =(n–1)knt
| 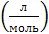 n–1 n–1
| 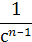
| 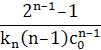
|
Эти закономерности позволяют определить порядок химической реакции.
|
|
Дата добавления: 2014-01-07; Просмотров: 1075; Нарушение авторских прав?; Мы поможем в написании вашей работы!