Несобственные интегралы от неограниченных функций

Пусть теперь функция f(x) задана на полуинтервале [a,b). Точку b будем называть особой, если функция f(x) не ограничена на [a,b), но ограничена на любом [a;b-a]Ì[a,b). Будем также предполагать, что на любом таком сегменте функция f(x) интегрируема.

В наших предположениях на [a;b-a] задана функция аргумента a .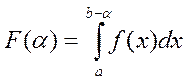

Исследуем вопрос о правом предельном значении функции F(x) в точке a=0, то есть вопрос о существовании предела:

.

При этом для обозначения этого выражения будем использовать обозначение: 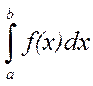. В дальнейшем этот символ будем называть несобственным интегралом второго рода от функции f(x) по полуинтервалу [a;b). Если указанный предел существует, интеграл будем называть сходящимся, если предел не существует или равен ¥, то интеграл будем называть расходящимся.

Аналогично для функции f(x), непрерывной на полуинтервале (a;b] и неограниченной вблизи а, вводится понятие несобственного интеграла .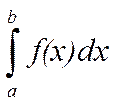

Полагают, что 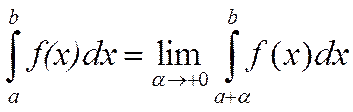, если этот предел существует и конечен.

Несобственный интеграл от функции f(x), непрерывной на интервале (a;b) и неограниченной вблизи его концов а и b, определяется равенством:

,

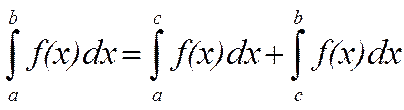где с – любая точка интервала (a;b), если каждый из несобственных интегралов 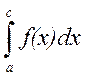и 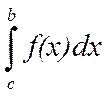сходится. При этом несобственный 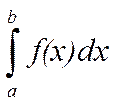называется сходящимся, его величина не зависит от выбора числа с. Если хотя бы один из интегралов 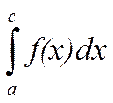и 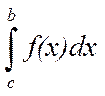расходится, то несобственный интеграл 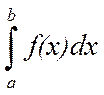называют расходящимся.

Пусть теперь функция f(x) непрерывна на отрезке [a;b] всюду, кроме некоторой точки с, a<c<b, и не ограничена вблизи с.

Несобственный интеграл 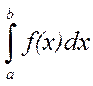определяется равенством 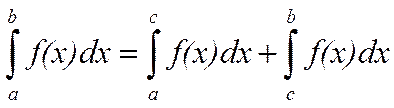, если каждый из интегралов в правой части равенства сходится. Если хотя бы один из этих интегралов расходится, то несобственный интеграл 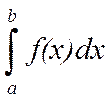называется расходящимся.

Аналогично определяется несобственный интеграл по отрезку [a;b] от функции, непрерывной на нем всюду, кроме конечного числа точек, и неограниченной вблизи этих точек.

Рассмотрим несколько примеров несобственных интегралов второго рода.

Дата добавления: 2014-01-20