Интегрируемость функции на сегменте

Определенный интеграл и его геометрические приложения

Пример 2.

Пример 1.

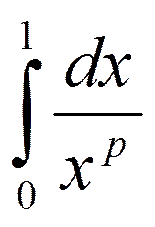, где р>0.

Это несобственный интеграл второго рода, так как 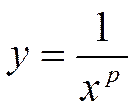, где р>0, – неограниченная на (0;1) функция: .

При р¹1: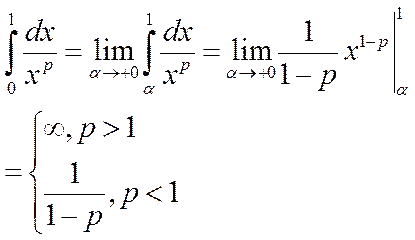

При р=1: .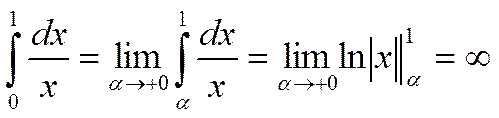

Таким образом, несобственный интеграл сходится при р<1 и расходится при р³1.

.

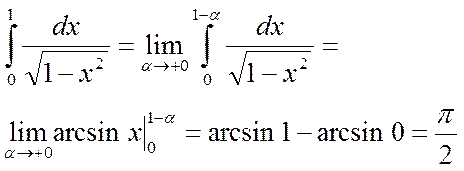Рис.1

Пусть функция f(x) задана на сег­менте [a,b] (a<b). Обозначим че- рез Т разбиение [a,b] при помощи не совпадающих друг с другом точек a=x0<x1<...<xn=b на n частич- ныхсегментов [x0,x1]...[xn-1, xn]. Точки x0,x1,...,xn называются точками разбиения Т. Пусть 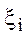- произвольная точка частичного сегмента [xi-1,xi]. Разность Dxi=xi -xi-1 будем называть длиной частичного сегмента [xi-1,xi].

Определение 1. Число , где

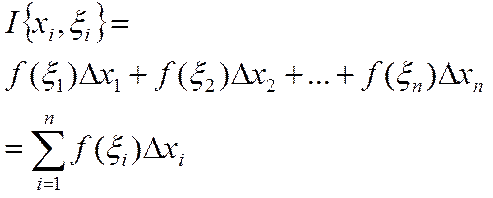
называется интегральной суммой функции f(x), соответствующей данному разбиению Т сегмента [a,b] и данному выбору промежуточных точек 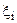на частичных сегментах [x_i-1,x_i].

Обозначим 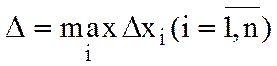- диаметр разбиения Т сегмента [a,b].

Геометрический смысл интегральной суммы 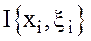. Рассмотрим криволинейную трапецию - фигуру, ограниченную графиком функции f(x) (будем считать ее положительной и непрерывной), двумя ординатами, проведенными в точках a и b оси абсцисс и осью абсцисс.

Интегральная сумма 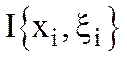- площадь ступенчатой фигуры (рис.1).

Определение 2. Число I называется пределом интегральных сумм 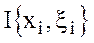при D®0, если для "e>0 можно указать такое положительное число 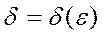, что для любого разбиения Т сегмента [a,b], максимальная длина D частичных сегментов которого <d, независимо от выбора точек 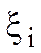на сегментах [x_i-1,x_i] выполнено неравенство

Если интегральная сумма 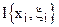при D®0 имеет пределом число I, то будем записывать это так .

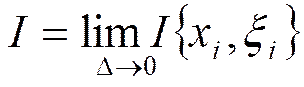Определение 3. Функция f(x) называется интегрируемой по Риману на [a,b], если существует конечный предел I интегральных сумм этой функции при D®0. Указанный предел I называется определенным интегралом функции f(x) по [a,b] и обозначается так:

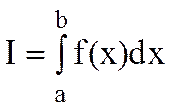
Из рисунка видно, что определенный интеграл численно равен площади криволинейной трапеции, определяемой графиком функции f(x) на [a,b].

Справедлива следующая

Т еорема. Неограниченная на [a,b] функция f(x) не интегрируема на этом сегменте.

Доказательство: Пусть функция f(x) неограничена на [a,b], тогда она не ограничена на некотором частичном сегменте [x_k-1,x_k] любого данного разбиения Т сегмента [a,b]. Тогда слагаемое f(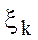)Dx_k интегральной суммы 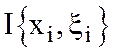, отвечающее этому разбиению Т, за счет выбора т.может быть сделано как угодно большим по абсолютной величине, т.е. интегральные суммы , отвечающие любому разбиению Т, не ограничены, и поэтому не существует конечного предела интегральных сумм. Итак, будем рассматривать лишь ограниченные на [a,b] функции.

Замечание: Отметим, что вообще говоря, не всякая ограниченная на [a,b] функция является интегрируемой на этом сегменте.

Проверьте это положение для функции Дирихле (значения в рациональных точках 1, а в иррациональных - 0). Эта функция не интегрируема на [a,b].

Дата добавления: 2014-01-20