Спрямляемость и длина дуги плоской кривой

Пусть заданы функции j(t) и y(t), непрерывные на сегменте [a,b]. Множество 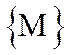всех точек М, координаты х и у которых определяются уравнениями 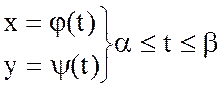называется простой кривой, если различным значениям параметра t из сегмента [a,b] отвечают различные точки этого множества.

Будем называть точки А и В, отвечающие граничным значениям a и b параметра t, граничными точками простой кривой. Простой замкнутой кривой называется кривая L, которая образуется объединением двух простых кривых L1 и L2 следующим образом:

1) граничные точки кривой L₁, совпадают с граничными точками кривой L₂; 2) любые не граничные точки кривых L₁ и L₂ различны.

Определение. Пусть j(t) и y(t) непрерывны на 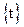. Уравнения

(1)

задают параметрически кривую L, если существует такая система сегментов 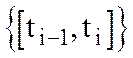, разбивающих множество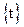, что для значений t из каждого данного сегмента этой системы уравнения (1) определяют простую кривую. При этом точки кривой L рассматриваются в определенном порядке в соответствии с возрастанием параметра t, т.е. если M₁ соответствует значению параметра t₁, а М₂ - t₂, то M₁ считаются предшествующей М₂, если t₁<t₂. Точки, отвечающие различным значениям параметра, всегда считаются различными.

Пример. Рассмотрим кривую L, задаваемую параметрически уравнениями

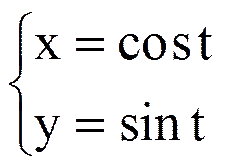(2)

0 £ t £ 4p. Это не простая кривая, но если взять систему сегментов [0, p], [p,2p], [2p,3p], [3p,4p], разбивающих [0,4p], то для значений t из каждого

указанного сегмента данной системы уравнения (2) определяют простую кривую (полуокружность). Кривая L - дважды обходимая окружность.

Итак, пусть кривая L задается параметрическими уравнениями . Пусть Т - произвольное разбиение [a,b] точками a₀=t₀<t₁<t₂<...<t_n = b. Соответствующие точки кривой L обозначим через М₀, М₁, М₂,..., М_n.

Ломаную M0M1M2...Mn будем называть ломаной, вписанной в кривую L и отвечающей данному разбиению Т сегмента [a,b]. Длина li звена Mi-1Mi этой ломаной равна

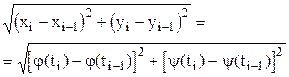
Длина 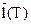всей этой ломаной равна

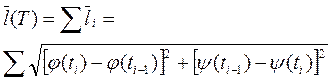
Определение. Если множество длин вписанных в кривую L ломаных, отвечающих всевозможным разбиением Т [a,b], ограничено, то кривая L называется спрямляемой. Точная верхняя грань l множества называется длиной дуги кривой L.

Теорема (о достаточных условиях спрямляемости и длине дуги плоской кривой). Если функции и 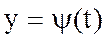имеют на сегменте [a,b] непрерывные производные, то кривая L, определяемая параметрическими уравнениями 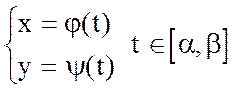, спрямляема, и длина l ее дуги может быть вычислена по формуле

.

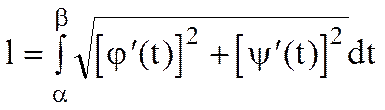Дата добавления: 2014-01-20