Функции многих переменных, заданные неявно

Чтобы найти наибольшее и наименьшее значение функции в замкнутой ограниченной области D нужно найти все внутренние точки D «подозрительные» на экстремум и сравнить со значениями функции в граничных точках области. Наибольшее (наименьшее) из этих значений и будет наибольшим (наименьшим) значением функции в области.

В замкнутой области.

Наибольшие и наименьшие значения функции

Пусть функция 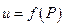определена и непрерывна в ограниченной замкнутой области D. По теореме Вейерштрасса, функция в этой области достигает наибольшего и наименьшего значения.

Примеры:

1°. Найти наибольшее значение функции в треугольнике:.

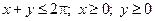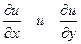Получаем: . Внутри области обращаются в ноль только в точке На границах области функция u = 0.

Наибольшее значение функции u (x, y):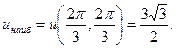

2⁰. Найти наибольшее и наименьшее значение функции: 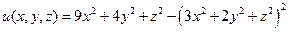при условии .

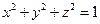а). Из условия: и, исключая из переменную получим:

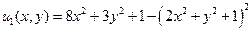. Сформулируем новую задачу:

Найти наибольшее и наименьшее значение функции в круге x ² + y ² 1.

;

.

Из необходимых условий следует, что:

а1). x = 0, y = 0; (= 0); а2). x = 0, y = ; (= 0,25);

а3). y = 0; x = (= 1); а4) .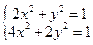

Последняя система, очевидно, решений не имеет.

б). Теперь надо посмотреть функцию на границе области, т. е. когда:

x ² + y ² = 1 Þ y ² = 1 – x ² Þ для .

Для нее: и, следовательно:

б1). x = 0; (= 0) б2). x = ; (= 0,25).

в). И, наконец, надо посмотреть точки x = ±1 при этом в1). x = ± 1, (= 0).

Вывод: наибольшее значение функции в области = = 1,

наименьшее значение = = = = 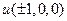0.

3°. Для функции одного переменного, если внутри промежутка имелось только одна точка локального экстремума, то в ней обязательно достигалось наименьшее либо наибольшее значение. Для функций многих переменных это, вообще говоря, не так.

Δ. Для примера рассмотрим функцию 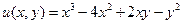в прямоугольнике: . Необходимые условия экстремума: , .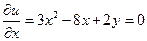

Отсюда следует: а1). x = 0, y = 0. а2). x = 2, y = 2 – не принадлежат прямоугольнику.

Достаточное условие экстремума в точке (0,0):

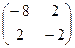=, D₁ = – 8; D₂ = 12.

Функция 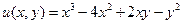в D имеет локальный максимум. И, при этом, 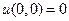. Однако это значение не является наибольшим в области, ибо: . ▲

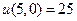А. Уравнение F (x ₁, x ₂,…, x _k, y) = 0 в (n+1) – мерном параллелепипеде:

a _i ≤ x _i ≤ b _i, i = 1, 2, 3…., n; c ≤ y ≤ d определяет y как однозначную функцию от x _i:

y = y (x ₁, x ₂, ….. x _n), если для любой точки (x ₁, x ₂, …. x _n) содержащейся в n -мерном параллелепипеде a _i ≤ x _i ≤ b _i, i = 1, 2, 3…., n уравнение имеет один и только один корень y в промежутке [ c, d ].

T^o. Пусть:

1. F (x ₁, x ₂,…… x _k, y) определена и непрерывна в (n + 1) – мерном параллелепипеде:

с центром в ,

2. Частные производные (i =1, 2,….., n) и существуют и непрерывны в D,

3. , 4. .

Тогда:

а. В некоторой окрестности уравнение 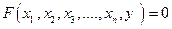определяет у как однозначную функцию y = f (x ₁, x ₂,… x _n),

б. При этом, ,

в. Функция y = f (x ₁, x ₂,… x _n) непрерывна по всем своим аргументам,

г. И имеет непрерывные частные производные , , ….., .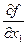

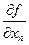Б. При каких условиях, в общем случае, система m уравнений:

(*)

определяет y ₁, y ₂,…, y _m как однозначные функции: ?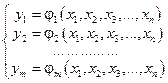

Ответ на этот вопрос дает следующая теорема, которая вместе с предыдущей носит название теоремы о неявных функциях.

T^o. Пусть:

1. Все функции F ₁(..), F₂(…), …. F _m(…) определены и непрерывны в (n + m) мерном параллелепипеде:

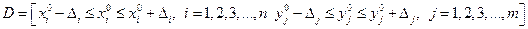
с центром в точке ,

2. Существуют и непрерывны в D частные производные всех функций F _j (…) по всем аргументам,

3. Точка удовлетворяет всем уравнениям системы (*),

4. Якобиан J системы в этой точке отличен от нуля.

J = = 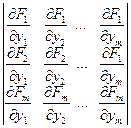¹ 0.

Тогда:

а. В некоторой окрестности точки система уравнений (*) определяет y ₁ = f ₁ (x ₁, x ₂,… x _n), y ₂ = f₂ (x ₁, x ₂,… x _n),…, y _m = f _m (x ₁,…, x _n), как однозначные функции от аргументов x ₁, x₂, …., x _n,

б. При этом, y _j⁰ = f _j (x ₁⁰, x ₂⁰, …, x _n⁰), j = 1, 2, …, m,

в. Функции f ₁, f ₂, …., f_m непрерывны в точке (x ₁⁰, x ₂⁰, …, x_n ⁰),

г. И имеют непрерывные частные производные по всем аргументам.

Дата добавления: 2014-01-11