Метод неопределенных множителей Лагранжа

Условные экстремумы функций многих переменных.

Постановка задачи: Требуется найти экстремумы функции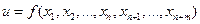

в предположении, что аргументы функции подчиняются m уравнениям связи:

(*)

Def. Функция 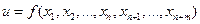имеет условный экстремум в , удовлетворяющей условиям связи (*), если в некоторой окрестности точки M ₀ для всех ее точек удовлетворяющих уравнениям связи (*) выполняется неравенство:

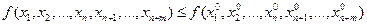(для максимума),

(для минимума).

Мы уже, по сути, решали такую задачу, когда из уравнений связи можно было найти отдельные переменные и, в последующем, исключать их из рассмотрения. В общем случае это удается сделать далеко не всегда.

Лагранж предложил метод нахождения экстремума функции 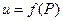, при наличии условий связи: 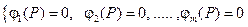, где .

Cоставим функцию (называемую функцией Лагранжа):

;

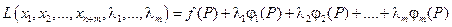*). Необходимые условия условного экстремума функции 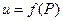с условиями связи (*) совпадают c необходимыми условиями экстремума (обычного) функции .

т.е. ; .

*). Достаточные условия условного экстремума функции 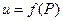это достаточные условия экстремума функции 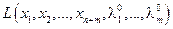где 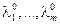– значения параметров в критической точке, т.е. фиксированы.

Пример:

1°. Найти экстремум функции , если .

Мы уже рассматривали эту задачу ранее и, при этом, выражали 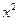через 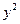. Если это невозможно сделать, выход из положения предлагает метод неопределенных множителей Лагранжа.

Составим функцию Лагранжа для решения задачи на условный экстремум:

.

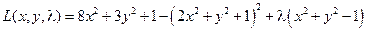Условный экстремум функции 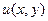совпадает с обычным экстремумом функции Лагранжа .

Необходимые условия экстремума:

;

; .

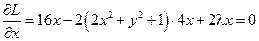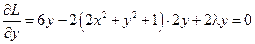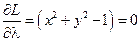Решая эту систему, найдем стационарные точки: 1). и

2). .

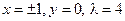В каждой из этих точек модифицируем функцию Лагранжа, подставляя соответствующее значение и проверим достаточные условия экстремума, составляя в найденных точках соответствующие матрицы из вторых производных.

1).

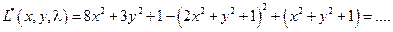
2).

Учитывая что:

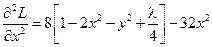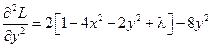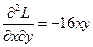; ; , запишем матрицы из вторых производных для каждой из стационарных точек и проверим достаточные условия экстремума:

1). 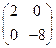. . Экстремума нет.

2). . . 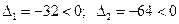Экстремума нет.

Вывод: Данная функция условных экстремумов не имеет.

2°. Найти экстремум функции 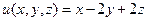, если .

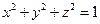На первом этапе решения задачи составим функцию Лагранжа:

.

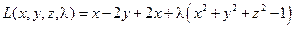Необходимые условия экстремума этой функции имеют вид:

; ; ; .

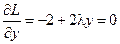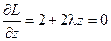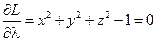Из первых трех уравнений следует, что:

.

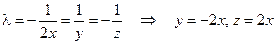Подставляя в четвертое уравнение, находим x, а затем, из полученных выше соотношений, находим и . Получаем две стационарные точки:

.

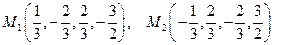Далее для каждой стационарной точки составляем модифицированную функцию Лагранжа. Для точки :

.

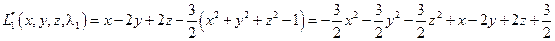Составляя матрицу из вторых производных, получаем:. Ее главные миноры чередуются по знаку, начиная с минуса. Следовательно, второй дифференциал модифицированной функции Лагранжа отрицателен и исходная функция в точке имеет условный максимум.

Для точки :

.

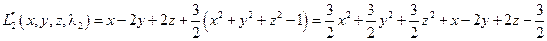Составляя матрицу из вторых производных, получаем: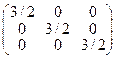. Все ее главные миноры положительны. Следовательно, второй дифференциал модифицированной функции Лагранжа положителен и исходная функция в точке имеет условный минимум.

2°. Найти наибольшееи наименьшее значение функции , при условии .

В этой задаче задано, не ограничение типа «равенство», как в предыдущей, а ограничение типа «неравенство». Поэтому задача решается в два шага.

а). Найдем экстремумы исходной функции в заданной области.

Из необходимых условий экстремума функции 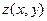следует:

.

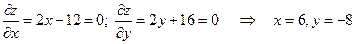Матрица из вторых производных 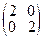имеет положительные главные миноры, положительный второй дифференциал и, следовательно, минимум в точке (6,–8). Этот факт, однако, нас совершенно не волнует, ибо точка (6,–8) не входит в рассматриваемую область.

б). Найдем теперь наибольшее и наименьшее значения исходной функции на границе области. Т.е. найдем наибольшееи наименьшее значение функции при условии .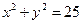

Теперь ограничение типа «неравенство», заменилось на ограничение типа «равенство» и, следовательно, имеем классическую задачу на условный экстремум.

Составляем функцию Лагранжа данной задачи:

Дата добавления: 2014-01-11