
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Начальные понятия и определения
|
|
|
|
.
Необходимые условия экстремума:
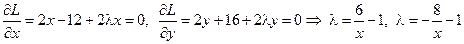 .
.
Находя из этих соотношений 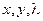 , получаем две стационарные точки:
, получаем две стационарные точки: 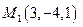 и
и 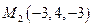 . Безусловно, можно установить характер экстремума в этих точках, однако, для нахождения наибольшего и наименьшего значения функции в этом нет никакой необходимости. Достаточно просто вычислить значения функции
. Безусловно, можно установить характер экстремума в этих точках, однако, для нахождения наибольшего и наименьшего значения функции в этом нет никакой необходимости. Достаточно просто вычислить значения функции 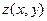 в найденных точках. Получаем
в найденных точках. Получаем 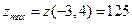 и
и 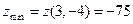 .
.
3°. Найти экстремум функции 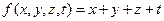 , при условии:
, при условии:
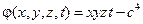 и область изменения переменных: x > 0, y > 0, z > 0, t > 0.
и область изменения переменных: x > 0, y > 0, z > 0, t > 0.
а). Функция Лагранжа: 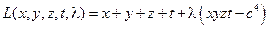 .
.
б). Необходимые условия экстремума функции Лагранжа:
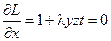 ;
; 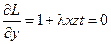 ;
; 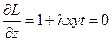 ;
; 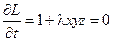 ;
; 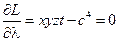 .
.
Отсюда: 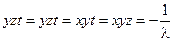 Þ
Þ 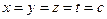 Þ
Þ 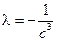 .
.
в) Преобразуем функцию Лагранжа, зафиксировав 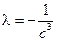 .
.
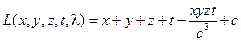 .
.
г). Для функции 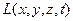 построим матрицу из вторых производных в окрестности точки
построим матрицу из вторых производных в окрестности точки 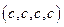 :
: 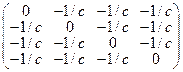 и, т.к. D1 = 0 то критерий Сильвестра ответа на вопрос о экстремуме не дает. При этом:
и, т.к. D1 = 0 то критерий Сильвестра ответа на вопрос о экстремуме не дает. При этом:
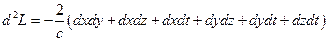 .
.
Находя дифференциал из уравнения связи, получаем: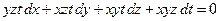 , что
, что
в окрестности особой точки равно: 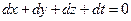 . Подставляя
. Подставляя 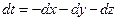 в
в 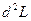 , получаем:
, получаем:
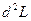 =
= 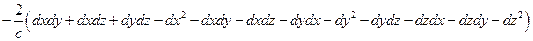 =
=
= 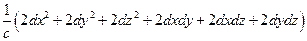 =
= 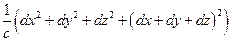 .
.
Ясно, что 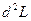 представляет собой положительно определенную квадратичную форму.
представляет собой положительно определенную квадратичную форму.
В точке 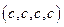 исходная функция
исходная функция 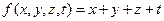 имеет условный минимум.
имеет условный минимум.
4°. Исследовать на наибольшее и наименьшее значение функцию:
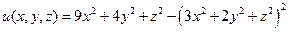 , при условии
, при условии 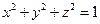 .
.
а). Функция Лагранжа:
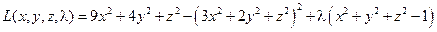
б). Необходимые условия экстремума функции Лагранжа:
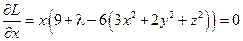 ;
; 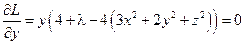 ;
;
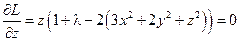 ;
; 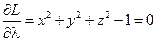 .
.
в). Решения этой системы:
*1. 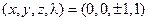 ; *2.
; *2. 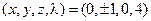 ;
;
*3. 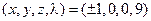 ; *4.
; *4. 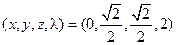 ;
;
*5. 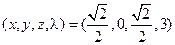 ; *6.
; *6. 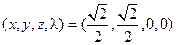 .
.
*7. Если 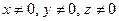 , то должны одновременно выполняться равенства:
, то должны одновременно выполняться равенства:
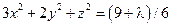 ;
; 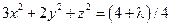 ;
; 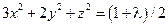 , что невозможно. Вычисляя значения функции
, что невозможно. Вычисляя значения функции 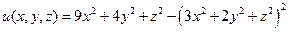 в найденных точках, находим наибольшее и наименьшее ее значения, при условии
в найденных точках, находим наибольшее и наименьшее ее значения, при условии 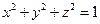 .
.
Обращаем внимание на то, что устанавливать имеется ли в критических точках экстремум, и каков характер этого экстремума (т.е. проверять достаточные условия) при решении задачи о наибольшем и наименьшем значении функции нет никакой необходимости.
Def. Пусть 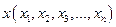 ,
, 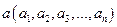 ,
, 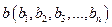
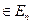 .
.
Множество 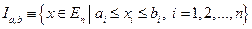 называется замкнутым промежутком или замкнутым брусом в
называется замкнутым промежутком или замкнутым брусом в 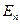 .
.
Множество 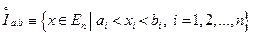 называется открытым промежутком
называется открытым промежутком
или открытым брусом в 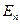 .
.
Def. Мерой промежутков 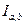 и
и 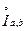 называется величина:
называется величина:
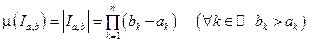 (Точнее
(Точнее 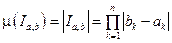 ).
).
Def. Если 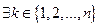 такое, что
такое, что 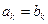 то промежуток
то промежуток 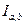 называется вырожденным и
называется вырожденным и 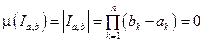 .
.
Свойства меры промежутка:
а). Положительность: 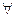
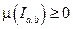 , причем
, причем 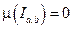 тогда и только тогда, когда
тогда и только тогда, когда 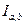 – вырожден.
– вырожден.
б). Положительная однородность: 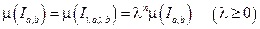 .
.
в). Аддитивность:
* для 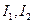 таких, что
таких, что 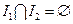 Þ
Þ 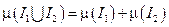 ;
;
* для 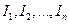 и
и 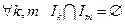 Þ
Þ 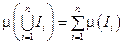 .
.
г). Монотонность меры: 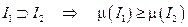 .
.
Def. Диаметром бруса (промежутка) называется величина:
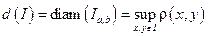
Отметим, что 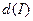 и
и 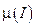 – это не одно и тоже. Например, если
– это не одно и тоже. Например, если 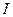 – вырожден, то
– вырожден, то 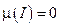 , a
, a 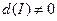 (вообще говоря).
(вообще говоря).
При этом: * 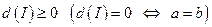 ;
;
* 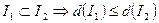 ; *
; * 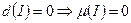 .
.
Def. Совокупность 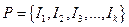 подпромежутков промежутка
подпромежутков промежутка 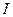 называется разбиением промежутка
называется разбиением промежутка 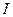 , если: *
, если: * 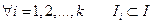 ;
;
* 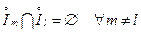 ; *
; * 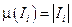 ; *
; * 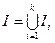 ; *
; * 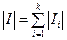 .
.
Величина 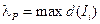 называется параметром разбиения P (при этом
называется параметром разбиения P (при этом 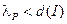 ).
).
Def. Разбиение 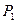 называется измельчением разбиения
называется измельчением разбиения 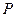 , если все элементы разбиения
, если все элементы разбиения 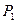 получены разбиением элементов разбиения
получены разбиением элементов разбиения 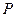 .
.
Обозначается: 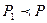 . Читается:
. Читается: 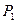 мельче
мельче 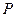 или
или 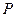 крупнее
крупнее 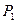 .
.
Для отношения “ крупнее – мельче” справедливо:
*. транзитивность – 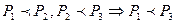 ; *.
; *. 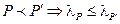 ;
;
*. 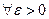
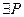
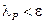 ; *.
; *. 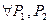
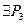 |
| 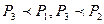 .
.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 415; Нарушение авторских прав?; Мы поможем в написании вашей работы!