Присоединение корня многочлена

Пусть P произвольное поле, P (x) - кольцо многочленов с коэффициентами из P. В кольце многочленов P (x) рассмотрим множество (f (x)) всех многочленов, делящихся без остатка на f (x). Множество (f (x)) образует двусторонний идеал. Элементами факторкольца P (x)/(f (x)) являются смежные классы. Каждый смежный класс состоит из тех и только тех многочленов, которые имеют одинаковый остаток от деления на f (x). Естественно, каждому смежному классу поставить многочлен наименьшей степени, который является остатком от деления всех многочленов этого класса на f (x). Пусть степень f (x) равна n. Тогда элементами факторкольца являются многочлены степени не выше n -1 с коэффициентами из P. Операции сложения и умножения в этом кольце сводятся к аналогичным операциям с остатками от деления на f (x).

Теорема 3.4. Факторкольцо P(x)/(f(x)) является полем тогда и только тогда, когда многочлен f(x) неприводим над полем P.

Доказательство. Если f (x) приводимый многочлен, то фактор кольцо содержит делители нуля, и, следовательно, не является полем. Пусть f (x) неприводимый многочлен. Для любого не нулевого многочлена g (x) степени меньше n НОД(f (x), g (x))=1, и, значит, найдутся такие многочлены u (x) и v (x), что u (x) f (x)+ v (x) g (x)=1. Но тогда 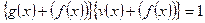, то есть для любого не нулевого элемента существует обратный к нему.

Пусть f (x) – неприводимый многочлен над полем P. Факторкольцо P (x)/(f (x)) является полем, и содержит все элементы поля P (точнее содержит подполе изоморфное P). Смежный класс { x +(f (x))} является корнем многочлена f (x). Действительно, при подстановке в f (x) получим смежный класс (f (x))=0. Таким образом, факторкольцо P (x)/(f (x)) кроме элементов P содержит корень многочлена f (x), и может рассматриваться как расширения поля P.

Пусть теперь f (x) произвольный многочлен. Разложим f (x) на неприводимые многочлены. Если хотя бы один из них имеет степень больше либо равную 2, то можно расширить исходное поле. Процесс расширения можно продолжать до тех пор, пока многочлен f (x) не будет разлагаться на линейные множители. Следовательно, любое поле P можно расширить до поля, в котором многочлен f (x) разлагается на линейные множители.

Дата добавления: 2014-01-11