Конечные поля

Теорема 4.2. Число элементов конечного поля pⁿ, где p – простое число.

Доказательство. Поскольку поле P конечно, то его характеристика отлична от нуля. Пусть p его характеристика. Поле P, можно рассматривать как векторное пространство над Z_p. Обозначим через v₁,…,v_n базис P. Любой элемент поля P однозначно характеризуется координатами (x₁,…,x_n) в этом базисе. Каждая координата принимает p значений, следовательно, число различных наборов координат, а значит и элементов поля P, равно pⁿ.

Лемма 4.1 В поле характеристики p .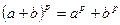

Доказательство. 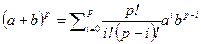, где 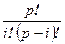- кратность вхождения элемента. Величина 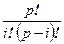не делится на p только в случае i= 0; p. Так как pe=0, то .

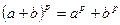Теорема 4.3. Для любого натурального n и простого p существует поле порядка pⁿ.

Расширим Z_p так, чтобы результирующее поле содержало все корни многочлена 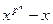. Многочлен не имеет кратных корней, так как его производная равна –1. Обозначим через M множество корней многочлена 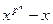. Легко проверить, что M является полем и число его элементов равно pⁿ

Теорема 4.4. Поле порядка 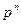единственно с точностью до изоморфизма.

Доказательство.

Поскольку число элементов поля 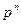, то его характеристика равна 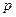. Следовательно, любое поле P порядка 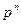можно рассматривать как расширение кольца вычетов 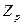. Мултьипликативная группа поля (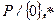) имеет порядок 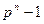, и, следовательно, для любого 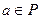справедливо 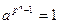. Таким образом, все элементы поля являются корнями уравнения 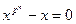над .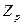

Теорема 4.5. Мультипликативная группа корней n -ой степени из 1 в поле P является цикличной.

Доказательство. Пусть p характеристика поля P. Если 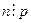, то 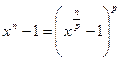, и, значит, множество корней уравнения 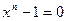совпадает с множеством корней степени 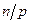. Не нарушая общности можно считать 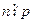. Доказательство достаточно провести для случая, когда все корни n -ой степени из 1 содержатся в поле P. В противном случае расширим поле и воспользуемся фактом, что любая подгруппа циклической группы – циклическая. Поскольку 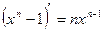имеет только единственный корень, равный нулю, то количество корней n -ой степени из 1 равно n. Рассмотрим три случая:

1. n – простое число. Тогда группа корней имеет порядок n, и, значит циклическая

2. 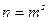- степень простого числа. Найдем корень 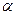уравнения 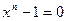, не являющийся корнем уравнения 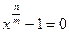. Порядок элемента 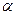является делителем порядка группы n и не является делителем 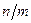. Следовательно, порядок 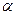равен n и группа циклическая.

3. Пусть 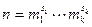. Обозначим через 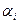порождающий элемент циклической группы корней из 1 степени 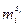. Положим 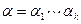. Индукцией по k покажем, что порядок 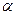равен 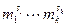. При k =1 утверждение очевидно. Пусть оно доказано для k -1. Порядок элемента 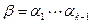равен 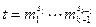. Наибольший общий делитель t и 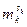равен 1, и, значит, найдутся числа u и v, что 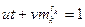. Поскольку 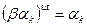и 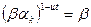, то порядок элемента 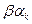делится на t и на 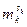. Далее, из равенства 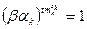, следует, что порядок элемента 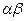является делителем . Теорема доказана.

Дата добавления: 2014-01-11