Примеры решения задач

О движении тел при торможении.

Обычно движение с возрастающей по модулю скоростью называют ускоренным движением. Движение с убывающей скоростью — замедленное движение. Но в механике любое движение с изменяющейся скоростью называют ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или тормозит (скорость уменьшается!), в обоих случаях он движется с ускорением. Ускоренное движение отличается от замедленного лишь знаком проекции вектора ускорения на координатную ось.

Если скорость тела с течением времени уменьшается (тело тормозится), то в какой-то момент времени скорость тела может стать равной нулю. Как оно движется после этого? Ясно, что, когда какая-либо величина, изменяясь, проходит через значение нуль, она изменяет свой знак на противоположный. В нашем случае изменяет знак скорость. Это значит, что после того, как скорость тела станет равной нулю, оно начнет двигаться в противоположном направлении (см. задачу 2 на с. 33).

1. Автомобиль проезжает мимо наблюдателя, двигаясь со скоростью 10 м/с. В этот момент водитель нажимает на тормоз и автомобиль начинает двигаться с ускорением, по модулю равным 1,0 м/с². Сколько времени пройдет до остановки автомобиля?

Решение. Выберем за начало отсчета координаты место нахождения наблюдателя, а координатную ось направим в сторону движения автомобиля (рис. 38).

Обозначим скорость автомобиля в момент, когда он проходит мимо наблюдателя, через v_o, а его ускорение после включения тормоза через а.

Воспользуемся формулой v_x = v_0x + a_xt. Здесь v_x, v_0x и а_х — соответственно проекции конечной скорости v, начальной скорости v₀ и ускорения а на ось X.

Скорость автомобиля сонаправлена с осью X, поэтому v_0x = v ₀, а так как скорость его уменьшается, то а_х— —а. В момент остановки v_x = 0. Следовательно, 0 = v₀ — at,

или at = v _о. Отсюда t = v₀:a. Подставив в это выражение значения v _о и а, получим

2. Тело движется прямолинейно с уменьшающейся скоростью. Ускорение а постоянно и по модулю равно 4 м/с². В некоторый момент времени модуль скорости тела vo =20 м/с. Найдите скорость тела через t₁ =4 с и t₂ = 8 с после этого момента.

Решение. Направим координатную ось X по направлению вектора скорости v₀. Тогда проекция v_ox положительна и равна модулю вектора v₀: v_0x = v_o. А так как скорость тела уменьшается, то проекция ускорения а_х отрицательна и равна —а: а_х— —а.

Чтобы найти проекцию скорости v_x в указанные в задаче моменты времени, применим формулу v_x = = v_0x + a_xt. Отсюда для момента времени t найдем:

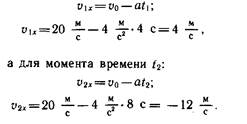
Знак «минус» означает, что к исходу 8-й секунды тело двигалось в направлении, противоположном начальному. Очевидно, что перед тем, как начать движение в обратном направлении, тело должно было остановиться. В какой момент времени t¹ это произошло?

Проекция (v_x равна нулю, когда)

5 с.

Направление движения изменилось на обратное через 5 с после того момента, когда скорость тела была равна 20 м/с.

Двигаться так, как описано в этой задаче, могло бы, например, тело, которое толкнули вверх по наклонной плоскости.

Упражнение 6 (4 задачи)

Дата добавления: 2014-01-14