Методические рекомендации 9 страница

или, направив ось z вдоль v:

n_zxn_y — Щ_уп_х = 0. (36,11)

Наконец, сделаем еще следующее замечание по поводу фигу­рирующих в (36,1) модулей упругости. Поскольку они введены как коэффициенты в свободной энергии, ими определяются изотер­мические деформации тела. Легко видеть, однако, что те же коэф­фициенты определяют в нематиках также и адиабатические де­формации. Действительно, мы видели в § 6, что для твердого тела различие между изотермическими и адиабатическими моду­лями возникает в силу наличия в свободной энергии члена, ли­нейного по тензору деформации. Для нематиков аналогичную роль мог бы играть член, линейный по производным d_hn_t. Такой член должен был бы быть скаляром и к тому же инвариантным по отношению к изменению знака п. Очевидно, что такой член по­строить нельзя (произведение n rot п — псевдоскаляр, а един­ственный истинный скаляр div п меняет знак вместе с п). По этой причине изотермические и адиабатические модули нематика совпадают друг с другом (подобно тому, как это имеет место для модуля сдвига изотропного твердого тела —§6). Эти рассужде­ния можно сформулировать и несколько иначе: в отсутствие ли­нейного члена квадратичная упругая энергия (36,1) является первой «малой поправкой» к термодинамическим величинам не-

деформированного тела; в силу «теоремы о малых добавках» (см. V, § 15), будучи выражена через соответствующие термоди­намические переменные (температуру или энтропию), она одина^ кова для свободной энергии и для внутренней энергии.

§ 37. Прямолинейные дисклинации в нематиках

Равновесному состоянию нематической среды при заданных граничных условиях не обязательно соответствует всюду непре­рывное распределение п (г), в котором вектор п имел бы в каждой точке вполне определенное направление. В механике нематиков необходимо рассматривать также и деформации с полями п (г), содержащими особые точки или особые линии, в которых направ­ление п оказывается неопределенным. Линейные особенности на­зывают дисклинациями.

Рис. 27

Возможность возникновения дисклинации можно проиллю­стрировать простыми примерами. Рассмотрим нематик в длинном цилиндрическом сосуде, причем граничные условия требуют перпендикулярности п поверхности сосуда. Естественно ожидать, что в равновесии вектор п в каждой точке будет лежать в пло­скости поперечного сечения цилиндра и направлен по радиусу в этом сечении (как это изображено на рис. 27, а); очевидно, что на оси цилиндра направление п будет при этом неопределенным, так что эта ось будет дисклинацией. Если же граничные условия требуют параллельности направления п стенке сосуда в пло­скостях его поперечного сечения, то установится распределение с векторами п, лежащими везде вдоль концентрических окруж­ностей в этих плоскостях с центрами на оси цилиндра (рис. 27, б); и в этом случае направление п на оси будет неопределенным.

Эти два примера — простые частные случаи прямолинейных дисклинации. Мы рассмотрим общую задачу о возможных рас­пределениях п (г) в прямолинейных дисклинациях в неограни­ченной нематической среде. Очевидно, что распределение п (г) в такой дисклинации не зависит от координаты вдоль ее длины, так что достаточно рассматривать его в плоскостях, перпенди­кулярных оси дисклинации. Будем считать, что и сам вектор п лежит везде в этих плоскостях. Таким образом, мы имеем дело с плоской задачей механики нематиков. Некоторые общие свой­ства решения этой задачи могут быть выяснены уже из общих соображений, без рассмотрения конкретных уравнений равно­весия.

Введем цилиндрическую систему координат г, ц>, г с осью г вдоль оси дисклинации. Как уже отмечено, распределение п (г)

не зависит от координаты г. Оно не "А ^ может зависеть также и от коорди-Ая^"^ наты г, поскольку в поставленной

>6 задаче (дисклинация в неограниченной

среде) нет никаких параметров с раз-мерностью длины, с помощью которых

f могла бы быть построена безразмерная

Рис. 28 (каковой является п (г)) функция пе-

ременной г. Таким образом, искомое распределение зависит только от угловой переменной: n = п (ср).

Введем угол между п и радиус-вектором, проведенным в плоскости г = const в данную точку (рис. 28); компоненты двух­мерного (в этой плоскости) вектора п:

n_r — cos «_ф = sin ч>.

Полярный угол ф отсчитывается от некоторого избранного на­правления в плоскости — полярной оси. Введем также угол д между п и полярной осью; очевидно, что 0 = ф + г|>.

Искомое решение определяется функцией гр (ф). Оно должно удовлетворять условию физической однозначности — при изме­нении переменной ф на 2л (т. е. при обходе вокруг начала коорди­нат) вектор п должен остаться неизменным с точностью до знака {изменение знака допустимо ввиду физической эквивалентности направлений п и —п). Это значит, что должно быть

О (Ф + 2л) = Ф (ф) + 2лл,

где п — целое или полуцелое положительное или отрицательное число (значение п = О отвечает «недеформированному» состоянию n = const). Для функции -ф (ф) = ■б — ф имеем отсюда

Ф (Ф + 2л) = 2л (п — 1) + ф (ф). (37,1)

Число п называют индексом Франка дисклинации.

Уравнение равновесия (которое будет выписано ниже) опреде­ляет производную dtyldy и имеет вид

его правая сторона не содержит независимой переменной ф — как следствие того, что уравнение должно быть инвариантно по отношению к любому повороту всей системы (нематика) как це­лого вокруг оси 2 (т. е. по отношению к преобразованию q> -*■ Ф + Фо); функция / (ijj) периодична с периодом я, поскольку значения f и ф -+- я физически тождественны. Отсюда

₄> = jf(x)dx, (37,3)

о

где постоянная интегрирования выбрана так, что ф = 0 при <р = 0. Подставив это выражение в (37,1), найдем, что

л

f = -i-|/_W^ = -^-r, (37,4)

о

при пф\ (черта означает усреднение по периоду функции).

Отсюда можно сделать важное заключение о симметрии дискли­нации: при повороте всей картины на угол ср₀ = 2я/2 (п — 1) вокруг оси 2 углы ф меняются на я, т. е. все распределение остается неизменным. Действительно, с учетом периодичности функции / (ф) это преобразование приводит к тождеству

ф-(-я i)j

Ф + -^ГТ= | Hx)dx = \f{x)dx+ | f(x)dx = _V + fn.

о о м>

Таким образом, в результате одного лишь требования однознач­ности ось z автоматически оказывается осью симметрии (С_т) порядка

т = 2|п — 11, пф\. (37,5)

«Линии тока» директора определяются как линии, в каждой точке которых элемент длины dt(dl_r = dr, dl_v = г d<f) паралле­лен п. Дифференциальное уравнение этих линий:

dydl_r = п_ф/п_г,

т. е.

■aftr-tg*. (37,6)

Отсюда видно, в частности, что среди линий тока имеются прямолинейные, на которых \|з = рп (р — целое число). Эти ли­нии представляют собой 21 п — 11 радиальных лучей

Ф = 1/1 — 1 \Р~Ч>р> Ф = Ря. р = 0, 1, 2, т — 1. (37,7)

Плоскость поперечного сечения дисклинации делится этими лу­чами на т одинаковых, повторяющих друг друга секторов.

Перейдем к конкретному построению решения для нематика, энергия деформации которого дается формулой (36,1)^х). Для плоского распределения имеем:

^div"= -т + "Г" = 4"^cos* <^[41]+ +')»

n rot n = О

(t|>' = dty/dqi). В свободной энергии остаются только члены с Кг и К, ^[42] ):

JF_drdrd<? =Щ«±j(j __acosЩ(1 + ^[43]),a=.

Интеграл no dr логарифмически расходится. В реальных за­дачах он обрезается сверху на некоторой длине R порядка вели­чины размеров образца. Снизу же интеграл обрезается на рас­стояниях порядка величины молекулярных размеров а, где пе­рестает быть применимой макроскопическая теория. При опре­делении интересующего нас решения на расстояниях а <^ г < R можно считать множитель

г t dr. R

L = -------- «In —

J г а

просто некоторой постоянной, так что равновесное распределение i|> (ф) определяется минимальностью функционала

2я

J (1 -acos2\|;)(l +г|/^[44])Лр = min. (37,8)

о

Уравнение Эйлера этой вариационной задачи:

(1 — a cos 2г|з) ip" = a sin 2гр (1 — ф'^[45]). (37,9)

Оно имеет, прежде всего, два очевидных решения:

гр = 0 (37,10)

^И гр = п/2. (37,11)

Это — осесимметричные решения, которым отвечают соответ­ственно рис. 27, а и рис. 27, б¹). Эти решения однозначны, т. е. индекс Франка этих дисклинации п = 1 (ср. (37,1)).

Для нахождения решений с пф \ замечаем, что уравнение (37,9) имеет первый интеграл²)

(1 -acos2y)0|/²- 1) = const s -Д-- 1. (37,12)

Отсюда находим решение в виде (37,3) с функцией

и ч Г 1 — a cos 2ip "1 ^!/2...

Константа q определяется условием (37,4)

<»-■>* Г [._:■"% г*-» №14)

о

(при этом должно быть |а|<7²<1). Эти формулы определяют искомое решение. При каждом п решение единственно: поскольку левая часть условия (37,14)—монотонно возрастающая функ­ция q, это равенство удовлетворяется лишь одним значением q. Функция f (х) четна; поэтому ср (ф) — нечетная функция. Это значит, что плоскость <р = 0 является плоскостью симметрии распределения; в силу существования оси симметрии С_т тем са­мым возникают еще т — 1 проходящих через ось г плоскостей симметрии. Наконец, плоскостью симметрии, очевидно, является плоскость 2 = 0. Таким образом, дисклинация с индексом и обладает полной симметрией точечной группы D_mft.

При п — 2 из (37,14) очевидным образом следует, что (7=1, и соответствующее решение есть просто

ф = _ф = т. (37,15)

Для выяснения качественного характера полученных реше­ний исследуем поведение линий тока вблизи радиальных лучей Ф ⁼ Фр (37,7). На этих лучах \|з = рп, а вблизи них ф «рп и функция (37,13) сводится к постоянной:

-&-/<*>«Ч1^Г^в*- ⁽³⁷'¹⁶>

Отсюда

ф - пр «-j- (ф - ф_р).

Дифференциальное уравнение линий тока принимает вид
din г,. 1 %

dq> ^{s Y} t — % ф — фр '

откуда находим для формы линий тока вблизи луча

г = consb|tp —• ф_р|\ (37,17)

Если ввести декартовы координаты с осью х вдоль луча, то вблизи последнего: г «х, ф — ф_р» ylx и уравнение линий тока запи­сывается в виде

# = const-jch-w. (37,18)

Далее надо рассмотреть различные случаи. При п ^ 3/2 имеем п — 1 > 0, и из (37,14) очевидно, что q > 0, и потому К > 0. В этом случае линии тока выходят -из начала координат, касаясь луча.

При п — 1/2 параметр q < 0, а с ним и МО. Численное исследование уравнения (37,14) показывает, что q² > 1, а потому и \К\ > 1. Из (37,18) видно, что у растет вместе с х. Область вблизи начала координат нельзя рассмотреть этим способом,

л = 5/2 л = 1/2 \\ П—1/2

- т=1. ГО-/ «Л ГП-3

{ г\<У (с—

! i \ "---Гг.

Рис. 29

так как, согласно (37,17), при X <; 0 малым значениям ф — ф_р отвечают большие значения г.

Наконец, при п < 0 параметр —1 <g X <3 0 и, согласно (37,18), у-*-0 при дс->оо. Линии тока асимптотически прижи­маются к лучу.

На рис. 29 схематически показаны линии тока для дисклина­ции с п = 3/2, п = 1/2 и п = —1/2.

§ 38. Несингулярное осесимметричное решение уравнений равновесия нематиков

Осесимметричные деформации (37,10—11) (см. рис. 27), пред­ставляющие дисклинации с индексом Франка п = 1, являются точными решениями уравнений равновесия нематической среды

S 38)

несингулярное осесимметричное решение 201

I\И//

1Л

i * $

\ « 1 v

с заданными граничными условиями на стенках сосуда. Однако они не являются единственными решениями этих задач. Они единственны только в категории плоских решений. Если же отка­заться от предположения о расположении векторов п везде в по­перечных к оси сосуда плоскостях, то возможны и другие реше­ния, причем не обладающие особенностью на оси. Так, если гра­ничные условия требуют перпендикулярности п стенке, то линии тока директора в таком решении без особенности расположены в меридиональных плоскостях и имеют показанную на рис. 30 форму. Начинаясь на стенке нормально к ней, линии тока изгибаются, стремясь к оси г = 0, на которой, таким образом, направление п оказы­вается вполне определенным. Более того, мы уви­дим, что отсутствие особенности в таком решении приводит к его большей термодинамической вы­годности (меньшей полной упругой свободной энергии) по сравнению с решением с особенностью на оси (P. Е. Cladis, М. Kleman, 1972). Присту­пим к построению этого решения.

Рис. 30

Будем искать осесимметричное, однородное вдоль оси г решение в цилиндрических коорди­натах г, ф, г в виде

n_t = cos % (г), п_ф = 0, п_г = sin х (г)

(38,1)

(смысл угла х показан на рис. 30). Граничное условие на стенке:

X = 0 при г = R (38,2)

(R —- радиус цилиндрического сосуда), а на оси поставим условие

X = я/2 при г = 0, (38,3)

₌__cosx-|_

rot^n =

отвечающее, как уже указано, отсутствию особенности. Имеем

dr

divn =

1 d(rn_T) r dr

Свободная энергия деформации (на единицу длины вдоль оси г) дается интегралом

j F_d2nrdr =

Ini?

= я J {(K_asln²x+/^sC₃cos^ax)x'² + ^iCOS^ax-/<iSin2x-x'US.

(38,4)

где штрих означает дифференцирование по переменной I = = In г!).

Первый интеграл уравнения равновесия (т. е. уравнения Эйлера вариационной задачи о минимуме функционала (38,4)):

sin² х + К, cos² х) Х'² - #i cos²х = const. (38,5) Согласно условию (38,3) должно быть % -*■ я/2 при £ -*■—со. Очевидно, что для этого должно быть %'• -*■ 0 при % -*■ я/2; поэтому const = 0, так что

^ХU_lSin²_x + K,cos²_X)^1/2 '

Отсюда находим искомое решение, удовлетворяющее условию (38,2), в виде

In — = -Д=- (1Ь«*х + К,и*У _{d (38i6)}

В противоположность дисклинации (37,10) это решение не авто-модельно: в него входит размерный параметр длины R. Интеграл (38,6) выражается через элементарные функции. Выпишем ответ в предположении, что К₈ > Кг'.

г ₌ г y^^-k'sbtjv i k _{arcsin sifl} л
я 1 Vl-k*sla*x +*'япх / 1 ^k>

(38,7)

иг_ K_s—Ki u'%_ i __ *,ss _

При г 0 разность я/2 — х стремится к нулю пропорционально первой степени г, а линии тока приближаются к оси г по экспо­ненциальному закону г ~ exp (const*г).

Для свободной энергии, связанной с этим решением, вычисле­ние дает

r

J F_d2nr dr = я/Ci {2 + ~- arcsin. (38,8)

о

Отметим, что это выражение вообще не зависит от радиуса со­суда R. Энергия же дисклинации (рис. 27, а; решение (37,10)):

я

| F_d2nrdr = nK_xL, (38,9)

^х) Последний член в подынтегральном выражении несуществен для форму­лировки вариационной задачи, но нужен для вычисления полной свободной энергии.

§ 38]

несингулярное осесимметричное решение 203

где L = In (R/a) — большой логарифм, происхождение которого связано именно с особенностью на оси. Мы видим, что решение без особенности энергетически более выгодно по сравнению с ре­шением с особенностью (если только коэффициент Kj. не аномально мал).

Поле п (г) рассмотренного здесь осесимметричного без особен­ности решения уравнений равновесия может быть получено из поля п (г) в дисклинации с п = 1 путем непрерывной (т. е. без возникновения каких-либо разрывов) деформации — постепен­ным выводим векторов п из плоскостей г — const. Это обстоятель­ство является проявлением весьма общей ситуации, которая будет выяснена в следующем параграфе.

Задачи

1. Найти осесимметричное решение уравнений равновесия нематической
среды в цилиндрическом сосуде без особенности на оси, отвечающее граничным
условиям рис. 27, б.

Решение. Ищем решение в виде

п_г = 0, = cos х (г), Пг = sin х М с граничными условиями

Х(Д) = 0, х(0) = я/2.

Имеем

го!_фп = —cosx-^-, rot_zn = -^y^ —sinx-^-, divn = 0. Свободная энергия:

J 2nrF_d dr = n j {K₂(sin X cos x — x')² + #з cos⁴ x) dl.

0 — oo

Первый интеграл уравнения равновесия:

Ktf,'* - № sin² х cos² х + К_я cos* х) = 0. Интегрирование этого уравнения приводит к результату (полагаем Kg > К₂).

# \Vl — № sin² х + a' sin х При г -*■ 0 угол х -*■ я/2 по закону

тг-*=²*'тг

Свободная энергия этой деформации R

| F$nr dr = пК_г J2 -f- -~- arcsin k\, о

между тем как свободная энергия плоской дисклинации рис. 27, б: nK^L.

2. Исследовать устойчивость дисклинации с индексом п = 1 относительно
малых возмущений вида бп (ф) (С. И. Ацисцмов, И. Е. Дзялошинский, 1972).

Решение, а) Невозмущенное поле радиальной дисклинации (рис. 27, а): я_г «= 1 я<р = п_г шв 0. Возмущенное же поле пишем в виде

«, «= cos в cos ф да 1 i- (6^а + ф^а), п_ф «я cos в sin ф я» ф, ге_г = sin 0 да 6,

где углы в и ф — функции угловой координаты <р. Энергия, связанная с этим возмущением:

j Far dr d(f = j {Д:,ф'2 ₊ /(₂0'a _{+ (/(8} _ /у фа _ д^а) _d(p. Для общего исследования надо было бы положить

СО 00

е(ф)- 2 9^"», ф(_ф)= 2 ф/⁸⁽р

и выразить энергию как функцию всех 6₄, Ф₈. Но и без того сразу видно, что рассматриваемая дисклинации всегда неустойчива относительно возмущения В„ (член — Л]9§ в энергии).

б) Невозмущенное поле циркулярной дисклинации (рио. 27, б): п_г = п_г == = 0, я,, = 1. Возмущенное поле записываем в виде

п, = cos b cos (-j- + Ф^» — Ф, п_% = cos ft sin + ф^ «1 —

- ~ (в* -f- ф²), п_г = sin е«е

(определение угла ф изменено по сравнению с предыдущим случаем). Соответ­ствующая энергия:

j F_dr**-*-j^{к*^(в'^{а + ф}'^{ь + ikx}~^к*^}^ ^{+ iki}~^{2кз)62}d<p-}

Наиболее «опасны» возмущения 6„ и ф₀; условия устойчивости по отношению к этим возмущениям:

Ki > K_s, Кг > 2К„.

Полученное в тексте и в вадаче 1 утверждение, что свободная энергия дефор­мации в дисклинациях с п = 1 превышае'1 энергию несингулярного осесимме-тричного решения означает лишь, что эти дисклинации могли бы быть в лучшем случае метастабильными. Теперь мы видим, что радиальная дисклинация вообще неустойчива, а циркулярная устойчива (относительно возмущений указанного вида) при соблюдении определенных соотношений между модулями.

3. Нематическая среда заполняет пространство между двумя параллель­ными плоскостями, причем граничные условия на одной плоскости требуют перпендикулярности, а на другой — параллельности директора поверхности. Определить равновесную конфигурацию п (г).

Решение. Равновесная конфигурация будет, очевидно, плоской; выбе­рем ее плоскость в качестве плоскости х, г с осью г перпендикулярной граничным плоскостям (плоскости z = 0 и г = к). Положим

««= sin % (г), n₂ = cos х (г). Свободная энергия деформации:

j Fa & = -y j {K_x sin» x + Kz cos* _X} X'^! a.

Первый интеграл уравнения равновесии.

(Дд sin² х + Кг cos² х) x'^z «=

откуда с учетом граничных условий

| (Ki sin^[46] х + Кг cos^[47] х)^1/2 d% = - J- J (Ki sfn^[48] x + cos^[49] x)^{1 /2} <*x.
о 0

или

где E (x, fe) — эллиптический интеграл второго рода.

§ 39. Топологические свойства дисклинации

Данное в § 37 определение индекса Франка было существенно связано с предположением о плоском характере деформации в дисклинации и однородностью вдоль ее длины. Покажем теперь, каким образом это понятие может быть введено в общем случае произвольных криволинейных дисклинации в нематической среде.

Энергия нематика не меняется при одновременном произволь­ном повороте директора во всех его точках. В этом смысле можно сказать, что состояния нематика вырождены по направлениям директора; эти направления играют роль параметра вырожде­ния. Введем понятие о пространстве вырождения — области до­пускаемого без изменения энергии изменения параметра вырожде­ния. Им является в данном случае поверхность сферы единичного радиуса, каждая точка которой отвечает определенному направ­лению п. Надо однако учесть еще, что состояния нематика, отли­чающиеся изменением знака п физически тождественны. Дру­гими словами, диаметрально противоположные точки на сфере физически эквивалентны. Таким образом, пространство выро­ждения нематика — сфера, на которой каждые две диаметрально противоположные точки считаются эквивалентными *).

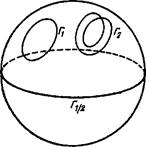
Представим себе, что мы производим в физическом объеме не­матика обход вокруг расположенной в нем дисклинационной ли­нии по некоторому замкнутому контуру (назовем его контуром у). Будем следить при этом обходе за направлением вектора п. Изображающая его точка в пространстве вырождения — на сфере — опишет некоторый тоже замкнутый контур (назовем его контуром Г). Здесь надо различать два случая.

В одном из них контур Г замкнут в буквальном смысле. Возвра­щаясь в исходное положение, изображающая точка описывает некоторое целое число п петель (так, для контуров Г\ и Г_а на рис. 31 это число равно 1 и 2). Это число и является целочислен­ным индексом Франка.

¹) Этому геометрическому образу отвечает в топологии так называемая

В другом случае контур Г, выйдя из некоторой точки на сфере, заканчивается в диаметрально противоположной точке. Такойконтур тоже должен рассматриваться как «замкнутый» ввиду эквивалентности диаметрально противоположных точек. Индекс Франка определяется как полуцелое «число петель», описываемых при этом изображающей точкой (так, для полуокружности Г1/2 это число п — 1/2).

Любой замкнутый контур на поверхности сферы может быть превращен в любой другой замкнутый контур путем непрерывной (т. е. без разрыва контура) деформации. Более того, любой замкну­тый контур может быть непрерывным образом стянут в точку ^[50]).

Также могут быть превращены друг в друга любые контуры, начинающиеся и кончающиеся в диаметрально проти­воположных точках сферы. Такие кон­туры, однако, не могут быть стянуты в точку: при деформировании концы контура могут смещаться, но лишь оставаясь при этом на концах какого-либо диаметра сферы.

Таким образом, индекс Франка не
является топологическим инвариан-
Рис. 31 том. Топологически инвариантен лишь

факт его цело- или полуцелочисленности. Из сказанного следует, что все дисклинации в нематической среде распадаются на две категории, в каждой из которых все дисклинации топологически эквивалентны — могут быть переве­дены друг в друга путем непрерывного деформирования поля п (г) (С. И. Анисимов, И. Е. Дзялошинской, 1972). Одну катего­рию составляют дисклинации с целыми индексами Франка; эти дисклинации к тому же топологически неустойчивы — они мо­гут быть вообще устранены путем непрерывного деформирования. Дисклинации целого индекса может заканчиваться в объеме не­матика.

Другую категорию составляют дисклинации с полуцелыми индексами. Эти дисклинации неустранимы, они топологически устойчивы.

Вопрос о том, какая из топологически эквивалентных струк­тур должна фактически осуществиться в тех или иных заданных условиях, зависит от относительной термодинамической выгод­ности этих структур. Это задача выходит за рамки топологического анализа.

Наряду с линейными особенностями, дисклинациями, в нема­тической среде могут существовать также и точечные особенности. Простейший пример такой особенности — точка, из которой тор­чат векторы п во все стороны («еж»).

$ 39] ТОПОЛОГИЧЕСКИЕ СВОЙСТВА ДИСКЛИНАЦИИ 207

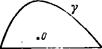
Для выяснения топологической классификации точечных осо­бенностей снова обратимся к отображениям в пространстве вы­рождения на единичную сферу. Выберем в заполненном немати-ком физическом пространстве две точки А и В, соединенные не­которым контуром Y, окружающим особую точку 0, как показано на рис. 32. На единичной сфере контуру у отвечает определенный контур Г. Будем теперь вращать контур у вокруг прямой АВ. После полного оборота, когда контур совместится сам с собой, он опишет в физическом пространстве замкнутую поверхность а. Ее отображение 2, описываемое контуром Г, покроет единич­ную сферу, возможно, более чем один раз. Число N покрытий единичной сферы отображением 2 является топологиче­ской характеристикой особой точки. Ото­бражение 2 можно представить себе как натянутую на сферу замкнутую пленку; очевидйо, что ее никак нельзя (не про­изводя на ней каких-либо разрезов) стя­нуть в точку. Этим выражается неустранимость особенности. Если N = 0, то пленка вообще не охватывает сферу. Это отве­чает отсутствию особенности или ее устранимости — такую плен­ку можно стянуть в точку. Для особых точек в нематике знак N не имеет смысла: его изменение означает лишь изменение направ­лений п во всем пространстве на обратные, что не отражается на состоянии нематика.

Число Л/, характеризующее точечную особенность, может быть только целым. Легко видеть, что полуцелое N означало бы в действительности существование неустранимой линейной, а не точечной особенности. Так, если 2 покрывает половину сферы (N = 1/2), то это значит, что, проследив за какой-либо одной точкой на у> мы найдем, что ее отображение описывает на сфере контур вида Г1/2 (рис. 31), что свидетельствовало бы о наличии неустранимой дисклинации с индексом Франка п=1/2^[51]).

В связи с обсуждением топологических свойств особенностей в нематиках остановимся кратко на топологическом истолковании дислокаций — особых линий в кристаллических решетках. Пред­ставим себе неограниченную кристаллическую решетку и введем оси х_ъ х_%, х₃, направленные вдоль трех основных периодов ре­шетки; величины этих периодов пусть будут a_lt а₂, а_я- Энергия решетки не меняется при ее параллельных сдвигах на любые рас­стояния вдоль осей х_ъ х_г, х_в. Области изменения параметров вы­рождения (величин сдвигов) — отрезки длины а_ъ о_а, а₃, причем у каждого отрезка обе его концевые точки рассматриваются как эквивалентные (поскольку сдвиг на период совмещает решетку саму с собой, т. е. оставляет состояние решетки тождественно неизменным). Отрезок с экивалентными концами топологически совпадает с окружностью. Таким образом, пространство вырожде­ния кристаллической решетки представляет собой трехмерную область, построенную на трех окружностях. Эту область можно представить себе как куб, противоположные грани которого по­парно эквивалентны, или, что то же самое, как трехмерную по­верхность тора в четырехмерном пространстве¹). На таком торе существуют не стягиваемые в точку контуры Г, каждый из ко­торых характеризуется тремя целочисленными топологическими инвариантами n_lt п₂, п₃ — числами обходов трех образующих тор окружностей. Если контур Г — образ контура у, обходящего в физическом пространстве особую линию (дислокацию), то три его инварианта совпадают с тремя компонентами вектора Бюр­герса (измеренными в единицах соответствующих периодов а_ъ а₂, а_я). Таким образом, дислокации —топологически устойчивые неустранимые особые линии, а их векторы Бюргерса —топологи­ческие инварианты.

Дата добавления: 2014-11-06