P.S. Не забудьте прихватить с собой небольшой сувенирчик. Будем обмениваться подарками. 10 страница

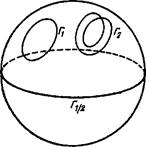
Любой замкнутый контур на поверхности сферы может быть превращен в любой другой замкнутый контур путем непрерывной (т. е. без разрыва контура) деформации. Более того, любой замкну­тый контур может быть непрерывным образом стянут в точку ^[50]).

Также могут быть превращены друг в друга любые контуры, начинающиеся и кончающиеся в диаметрально проти­воположных точках сферы. Такие кон­туры, однако, не могут быть стянуты в точку: при деформировании концы контура могут смещаться, но лишь оставаясь при этом на концах какого-либо диаметра сферы.

Таким образом, индекс Франка не
является топологическим инвариан-
Рис. 31 том. Топологически инвариантен лишь

факт его цело- или полуцелочисленности. Из сказанного следует, что все дисклинации в нематической среде распадаются на две категории, в каждой из которых все дисклинации топологически эквивалентны — могут быть переве­дены друг в друга путем непрерывного деформирования поля п (г) (С. И. Анисимов, И. Е. Дзялошинской, 1972). Одну катего­рию составляют дисклинации с целыми индексами Франка; эти дисклинации к тому же топологически неустойчивы — они мо­гут быть вообще устранены путем непрерывного деформирования. Дисклинации целого индекса может заканчиваться в объеме не­матика.

Другую категорию составляют дисклинации с полуцелыми индексами. Эти дисклинации неустранимы, они топологически устойчивы.

Вопрос о том, какая из топологически эквивалентных струк­тур должна фактически осуществиться в тех или иных заданных условиях, зависит от относительной термодинамической выгод­ности этих структур. Это задача выходит за рамки топологического анализа.

Наряду с линейными особенностями, дисклинациями, в нема­тической среде могут существовать также и точечные особенности. Простейший пример такой особенности — точка, из которой тор­чат векторы п во все стороны («еж»).

$ 39] ТОПОЛОГИЧЕСКИЕ СВОЙСТВА ДИСКЛИНАЦИИ 207

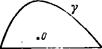
Для выяснения топологической классификации точечных осо­бенностей снова обратимся к отображениям в пространстве вы­рождения на единичную сферу. Выберем в заполненном немати-ком физическом пространстве две точки А и В, соединенные не­которым контуром Y, окружающим особую точку 0, как показано на рис. 32. На единичной сфере контуру у отвечает определенный контур Г. Будем теперь вращать контур у вокруг прямой АВ. После полного оборота, когда контур совместится сам с собой, он опишет в физическом пространстве замкнутую поверхность а. Ее отображение 2, описываемое контуром Г, покроет единич­ную сферу, возможно, более чем один раз. Число N покрытий единичной сферы отображением 2 является топологиче­ской характеристикой особой точки. Ото­бражение 2 можно представить себе как натянутую на сферу замкнутую пленку; очевидйо, что ее никак нельзя (не про­изводя на ней каких-либо разрезов) стя­нуть в точку. Этим выражается неустранимость особенности. Если N = 0, то пленка вообще не охватывает сферу. Это отве­чает отсутствию особенности или ее устранимости — такую плен­ку можно стянуть в точку. Для особых точек в нематике знак N не имеет смысла: его изменение означает лишь изменение направ­лений п во всем пространстве на обратные, что не отражается на состоянии нематика.

Число Л/, характеризующее точечную особенность, может быть только целым. Легко видеть, что полуцелое N означало бы в действительности существование неустранимой линейной, а не точечной особенности. Так, если 2 покрывает половину сферы (N = 1/2), то это значит, что, проследив за какой-либо одной точкой на у> мы найдем, что ее отображение описывает на сфере контур вида Г1/2 (рис. 31), что свидетельствовало бы о наличии неустранимой дисклинации с индексом Франка п=1/2^[51]).

В связи с обсуждением топологических свойств особенностей в нематиках остановимся кратко на топологическом истолковании дислокаций — особых линий в кристаллических решетках. Пред­ставим себе неограниченную кристаллическую решетку и введем оси х_ъ х_%, х₃, направленные вдоль трех основных периодов ре­шетки; величины этих периодов пусть будут a_lt а₂, а_я- Энергия решетки не меняется при ее параллельных сдвигах на любые рас­стояния вдоль осей х_ъ х_г, х_в. Области изменения параметров вы­рождения (величин сдвигов) — отрезки длины а_ъ о_а, а₃, причем у каждого отрезка обе его концевые точки рассматриваются как эквивалентные (поскольку сдвиг на период совмещает решетку саму с собой, т. е. оставляет состояние решетки тождественно неизменным). Отрезок с экивалентными концами топологически совпадает с окружностью. Таким образом, пространство вырожде­ния кристаллической решетки представляет собой трехмерную область, построенную на трех окружностях. Эту область можно представить себе как куб, противоположные грани которого по­парно эквивалентны, или, что то же самое, как трехмерную по­верхность тора в четырехмерном пространстве¹). На таком торе существуют не стягиваемые в точку контуры Г, каждый из ко­торых характеризуется тремя целочисленными топологическими инвариантами n_lt п₂, п₃ — числами обходов трех образующих тор окружностей. Если контур Г — образ контура у, обходящего в физическом пространстве особую линию (дислокацию), то три его инварианта совпадают с тремя компонентами вектора Бюр­герса (измеренными в единицах соответствующих периодов а_ъ а₂, а_я). Таким образом, дислокации —топологически устойчивые неустранимые особые линии, а их векторы Бюргерса —топологи­ческие инварианты.

§ 40. Уравнения движения нематиков

Состояние движущейся нематической среды определяется рас­пределениями в пространстве четырех величин: директора п, плотности массы р, скорости v и плотности энтропии S. Соответ­ственно этому полная система гидродинамических уравнений движения нематика состоит из четырех уравнений, определяющих производные по времени от указанных величин (J. L. Eriksen, 1960; F_t м: Leslie, 1966)^а).

Начнем с уравнения для директора. Если нематик находится в равновесии (так что h — 0) и движется как целое с постоянной по пространству скоростью, то это уравнение должно выражать собой просто тот факт, что и значения п переносятся в простран­стве с той же скоростью. Другими словами, каждая жидкая час­тица перемещается в пространстве со своим значением п. Это выражается равенством нулю полной (или, как говорят, суб­станциональной) производной по времени

4^L=-l^L+(^vv)ⁿ=ⁱ⁰- (ад

^г) Подобно тому, как квадрат с попарно эквивалентными противоположными сторонами топологически эквивалентен двухмерной поверхности тора в трех­мерном пространстве.

В общем же случае произвольного движения в правой части уравнения появляются члены, зависящие от h и от производных

$ 40]

уравнения движения нематиков

скорости по координатам; в первом неисчезающем гидродинами­ческом приближении надо ограничиться членами, линейными по этим величинам. Производные dv_t/dx_h составляют тензор, кото­рый можно разделить на симметричную и антисимметричную части:

v_ih = Vi (div_h + d_hv_t), Q_tk = V₂ (d_tv_h - d_hv_t). (40,2)

Для установления зависимости от Q_ik достаточно заметить, что при равномерном вращении нематика как целого с угловой ско­ростью Q, с той же скоростью будет вращаться и все поле п(г). Такое вращение описывается уравнением

-^-=4-[rotv.n] или ^- ₌ Q_ktn_k.

Действительно, скорость точек вращающегося как целое тела v = [Qr]; тогда rot v = 2Й и для скорости изменения директора получается такое же выражение dnldt — [Qn]. Члены же, зави­сящие от v_ik, должны быть составлены с учетом требования n dn/dt = 0, следующего из постоянства квадрата n^a = 1. Таким образом, приходим к следующему общему виду «уравнения дви­жения директора»:

•4т=Q_hin_k + X {б_и — щщ) n_hv_hl + N_u (40,3)

где ^г)

N = Ыу. (40,4)

Член N описывает релаксацию директора к равновесию под дей­ствием молекулярного поля, а второй член в (40,3)—ориенти­рующее действие градиента скорости на директор. Коэффициент у (с размерностью вязкости) и коэффициент % (безразмерный) в этих членах имеют кинетическую (а не термодинамическую) природу ^[52]).

Уравнение для временной производной плотности жидкости есть уравнение непрерывности

-|^+div(pv) = 0. (40,5)

Отметим, что этим уравнением, по существу, определяется гидро­динамическая скорость как плотность потока вещества, отнесен­ная к единице его массы.

Уравнение для временной производной скорости есть дина­мическое уравнение

p4- = ^F> (40,6)

^х) Обозначение N введено для более ясного выявления структуры некоторых формул ниже, а также ввиду дальнейших обобщений в § 43.

^а) Отсутствие в правой стороне уравнения (40,3) членов с градиентами плот­ности и энтропии (или температуры) связано с требованиями инвариантности уравнений по отношению к пространственной инверсии и по отношению к изме­нению знака п. См. об этом подробнее в § 43.

где F —сила, действующая на единицу объема. В соответствии с изложенными в § 2 общими рассуждениями, объемные силы мо­гут быть представлены в виде тензорной дивергенции

Ft = d_ka_ik,

где o_ih — тензор напряжений. Тогда динамическое уравнение запишется в виде

P-^-^EP(-^ + (vV)0i) = d_Aa_ib. <⁴⁰'⁷⁾

Вид тензора напряжений будет установлен ниже.

Наконец, остается еще уравнение для энтропии. В отсутствие диссипатив.ных процессов движение жидкости было бы адиаба-тичным, причем адиабатичным в каждом элементе жидкости, ко­торые передвигались бы со своими постоянными значениями энтропии. Уравнение, выражающее сохранение энтропии, запи­сывалось бы просто в виде уравнения непрерывности для нее:

-g-+div(Sv)= 0,

где S — энтропия единицы объема, а vS — плотность потока энтропии ¹). При учете диссипативных процессов энтропийное уравнение имеет вид

-§-+div(Sv + -f-)--^-. (40,8)

Здесь R — так называемая диссипативная функция; 2R/T опре­деляет скорость возрастания энтропии ²); она представляет собой квадратичную форму, составленную из компонент тензора v_lh и векторов h и градиента температуры у Т. Вектор же q — плотность потока тепла, связанного с теплопроводностью. Компоненты этого вектора — линейные функции компонент вектора градиента температуры

4i = - [53] vAT. (40,9)

В нематической среде тензор коэффициентов теплопроводности x_jft имеет две независимые компоненты и может быть представлен в виде

*) Это уравнение может быть представлено в эквивалентном виде выражающем постоянство переносимой частицами жидкости энтропии, отнесенной к единице массы.

Щн = хцЯ,-п[54] -f Xj. (6ik — п_сп_к), (40,10)

где и ц и х_х описывают теплопроводность в продольном и попе­речном (по отношению к п) направлениях.

Закон сохранения энергии в гидродинамике выражается уравнением вида

4-[-^l+£]+divQ= 0, (40,11)

где Е — плотность внутренней энергии, a Q — плотность потока энергии. Плотность энергии Е = Е₀ -f E_d, где £„ (P. S) отно­сится к недеформированной, однородной среде, а энергия E_d свя­зана с искажением поля п (г). Согласно сказанному в конце § 36 величина E_d совпадает со свободной энергией F_d (36,1), с той лишь разницей, что модули упругости К\, Кг, Ks подразу­меваются выраженными через плотность и энтропию, а не тем­пературу.

Закон сохранения энергии содержится, конечно, в уравнениях движения. Мы же воспользуемся им для установления связи между введенными выше функцией R, тензором a_ik и вектором N.

Раскроем производную по времени в уравнении (40,11) с уче­том термодинамических соотношений

{'ж)_Р,и^==Т' (~|r)s,n ^{= ,A}' где р — химический потенциал [55]). Имеем

dt ^£J ~ 2 ^T+P^v dt +^1Г+ ¹ dt + V dt)_P,s-

(40,12)

Рассмотрим отдельно последний член. Введя обозначение n_ki из (36,6), пишем

/ дЕ_л \ (dE_d \ Jnt,, dn_t
\~dT)p.S⁼⁼ \~ЗпТ)_р,8~дГ + ST ⁼

(вместо Н здесь написано h, поскольку продольная часть Н сразу выпадает ввиду равенства ndn/dt = 0). Подставив сюда dn/dt из (40,3), пишем:

(цг)_{р s} = (о[56] d_hn_t + Q_ikn_h - Xv_thn_h) А, - Nh + div (• • •)и после выделения еще одной полной дивергенции;

(T)_p,_s = -^Gv-T^{/l2 + div(}-'-)' ⁽⁴⁰'¹³⁾

где

G_t = - h_hd_tn_h -f- -±-d_h (n,h_h — n_kh_t) — -^-d_h (n_th\ + n_hh_t). (40,14)

Здесь и ниже мы не выписываем полностью выражение под зна­ком дивергенции с целью уменьшения громоздкости формул1 Эти члены (к которым мы вернемся еще в конце параграфа) не существенны для решения поставленного вопроса. Выражение (40,14) можно представить в виде

Gt^dboti + frE&.s, (40,15)

где

а\ь = — n_ki ditii — ~ (tiih_k + n_khc) + (n_ch_k — n_kh_t). (40,16)

При преобразовании использовано равенство

дЕ

(diE_d)_p, _s = d_tn_h + n_lh d_t d_tn_h.

Определение тензора ofk неоднозначно! выражение (40,15) не изменится при добавлении к ofy любого слагаемого вида di%_tt_h, где Хин — произвольный тензор, антисимметричный по послед­ней паре индексов (%_tlk = —Хотя тензор (40,16) не симме­тричен, он может быть приведен к симметричному виду прибавле­нием члена указанного вида с надлежащим образом подобранным тензором %u_h. Фактическое проведение этой, довольно громоздкой, операции отложим до конца параграфа, а сейчас продолжим вывод уравнений движения, предполагая симметризацию 0$ уже произведенной.

Подставив (40,15) в (40,13) и выделяя в одном из членов пол­ную дивергенцию (с учетом симметричности o\^r_k^}), получим ^[57])

(-^-)_pS=-Nh + a|^-(a^)p,_s^+div (...)• (40,17)

Наконец, подставим в (40,12) фигурирующие там производные по времени из (40,5), (40,7—8) и (40,17), причем частную (при по­стоянных р и S) производную от Е выразим через полную произ­водную согласно

§ 403

уравнения движения нематиков

После ряда преобразований (выделения полных дивергенций) получим в результате

4- [-т^[58] +^Е]=-^а«°'* -^Nh+4-^qVT+^2R+^div(*'

(40,18)

где offe связано с а«формулой

а«= - рЬ_1к+ аЯ> + а«, (40,19)

а давление введено согласно его термодинамическому опреде­лению;

р = рр — Е + TS (40,20)

(рр> == Ф — термодинамический потенциал единицы объема ве­щества); как и должно было быть, им определяется изотропная часть тензора напряжений.

Сравнив (40,18) с уравнением сохранения энергии (40,11), мы видим, что

2R = a'ikVik -f- Nh - -jr qV7\ (40,21)

Эта функция определяет вызванное диссипативными процессами увеличение энтропии. Ясно поэтому, что введенный в (40,19) тензор oik представляет собой диссипативную («вязкую») часть тензора напряжений. Тензор же crj^ в (40,21) не входит; он пред­ставляет собой недиссипативную (помимо связанной с давлением) часть тензора напряжений ^[59]), специфическую для нематической (в отличие от обычной) жидкости.

Обратим также внимание на то, что в диссипативную функцию не входит коэффициент к. Хотя описываемый этим безразмерным коэффициентом эффект имеет явно кинетическую (а не термодина­мическую) природу, он не диссипативен ^[60]).

Плотность объемных сил в движущейся нематической среде

Ft = - d_iP + дно® + dko'i_k = - dtp + FP +F'_t.

В неподвижной равновесной (хотя и деформированной) среде F' = 0, а согласно условию равновесия (36,7) и h = 0. Согласно (40,14—15) при этом еила

F⁽'> = - (V£_d)_p. _s, F=—V> — (V£_d)_p, _s.

Если считать модули упругости постоянными, не зависящими от р и S величинами, то (V£_d)p,_s = VE_d и тогда сила F = = —V (р -f- Е_а). Но в равновесии должно быть также и F = 0.

Отсюда следует, что (в указанном предположении).распределение давления вдоль находящейся в равновесии нематической среды дается формулой ^х)

р = const — Е_А. (40,22)

Произведем теперь в явном виде упомянутую выше операцию симметризации тензора о$■ Прежде всего, вычислим в явном виде антисимметричную часть этого тензора. При вычислении разности а$ — oi? надо учесть, что выражение

B_lh = -Цг- Ч + я» d_tn_h - n_kl a,n,

симметрично по индексам i, k. Проверить эту симметрию непо­средственно нелегко. Проще сделать это косвенным путем, вос­пользовавшись тем, что энергия E_d — скаляр и тем самым инва­риантна относительно произвольных вращений системы коорди­нат. При бесконечно малом повороте на угол б<р координаты пре­образуются как

г' = г + 6г, бг = [бф-г],

т. е.

ox_t = 8_(ft%, &_ih = е„_л8ф_г = — 8_ft,.

Для изменения вектора п и тензора d_fen, имеем соответственно бл, = в„п„ 6 (d_hn_t) - е,_г d_hn_t -f e_ft; <Э_гл,.

Инвариантность функции Е_й при этом повороте означает, что B_ihe_lh — 0. Поскольку e,_ft — произвольный антисимметричный тензор, то отсюда следует, что B_ik — симметричный тензор, что и требовалось доказать.

Имея это в виду, легко привести антисимметричную часть тензора e\^rit к виду (2,11) с тензором

Фш = n_tn_lk — П_кПц.

После этого симметризованный тензор aft} получается непосред­ственно по формуле (2,13). После некоторых приведений получим

¹) Если не делать указанных предположений, то силу F при постоянной температуре можно привести к виду F = —р Vu, так, что условие равновесия сводится к обычному р. = const. Действительно, дифференцируя выражение (40,20) для давления и учитывая термодинамическое соотношение dE = Т dS -f-+ p. dp + (dE_d)p, s, найдем — Vp = -pV(i - SVT -f (VE_d)_Pl g, откуда при T = const и получается указанное выражение для F.

~~Y^di [(Щк + я*,) Щ - n_klni — щ_гп_к]. (40,23)

41]

диссипативн ые коэффициенты нематиков 215

Отметим, что это выражение фактически содержит только попереч­ные (по индексу k) компоненты тензора n_ik. Если представить последний в виде

(так что n^fik = 0), то в (40,23) останутся только члены с пи-Наконец, вернемся к членам с полными дивергенциями, кото­рые мы до сих пор не выписывали. Сравнив (40,18) с (40,11), видим, что выражение, стоящее под знаком div в совокупности этих членов, определит собой плотность потока энергии. Приведем здесь получающийся таким образом окончательный результат:

Qi = (№ + -у)»i - n_ih \— Vi 6>й + ®ф1 + И fat — n_hn_mVi_m)\ +

1 X

4- -j- (tiih_k — n_khi) v _k + -y {ttihk + n*A<) «4 — alkVk — *ik д_кТ,

(40,24)

где W = p + E — тепловая функция. Первый член совпадает с выражением потока энергии в гидродинамике обычной жидкости.

§ 41. Диссипативные коэффициенты нематиков

Члены с N и a'ii в уравнениях движения выражают собой релаксационные процессы, возникающие вследствие термодина­мической неравновесности среды; эта неравновесность в свою очередь связана с отличными от нуля h и v_tk. В обычном гидроди­намическом приближении неравновесность предполагается сла­бой, т. е. величины h, v_ik — в определенном смысле малыми. Тогда о'сь является их линейными функциями.

Однако при принятой нами форме записи уравнений движения зависящих от h членов в o'_ik писать не надо. Действительно, такие члены, составленные из компонент h и п, имели бы вид const- (n_th_k + n_hh_t). Но член такого вида уже есть в недиссипа-тивной части тензора напряжений о$ (40,23); добавление по­добного члена в а'_{к сводилось бы поэтому лишь к переопределе­нию коэффициента А,.

Общий вид линейной зависимости oik от y^i

Oik = r\_ik,_mV lm, (41,1)

причем тензор четвертого ранга т)_Шт обладает очевидными свой­ствами симметрии (следствиями симметрии тензоров oik и vtk)

ЛШт = ШИтп — Thftm!- (41.2)

Кроме того, этот тензор обладает и более глубокой симметрией, следующей из общего принципа симметрии кинетических коэффи­циентов Онсагера (см. V, § 120; как и в § 32, ниже в этом параграфемы пользуемся формулировкой этого принципа, данной в VI § 59 и введенными там определениями величин х_а и Х_а). Из выраже­ния 2R/T для скорости увеличения энтропии видно ^[61]), что если под величинами х_а понимать компоненты тензора a'_ik, то «термо­динамически сопряженными» с ними величинами Х_а будут ком­поненты тензора — v_lmIT^[62]). Компоненты же тензора Цшт играют роль кинетических коэффициентов у_аЬ. Принцип Онсагера требует равенств у_аЬ = у_Ьа, т. е.

Пшш = Штл- (41.3)

Тензор r\_iki_m должен быть составлен лишь с помощью единич­ного тензора o_lh и вектора п с учетом указанных свойств симмет­рии. Имеется всего пять линейно независимых таких комбинации

"гп_йл_г«_т, n_tn_h6_lm + tiin_mb_th, ЩпА_т -f n_knA_m + л*п_т6_йг + h_hnj>_lb

fyftfym, ^[63]i Am + Ь_мЪ_1т.

Соответственно тензор r\_ihlm имеет пять независимых компонент; представим составленный с его помощью тензор напряжений в виде ^[64])

O'ik = 2T)it>«+ (П2 — T]l) O_ikVii +

+ (TU +!h — Пг) (o_ihnin_mv_lm + n,n_ko„) +

+ (Us - 2гц) {n_tniv_hl + n_kniv_ti) -f-

+ (Tls + Th + Th — 2г|з- 2т)₄) л,/г_й«_гл_гоог_т- (41,4)

Целесообразность именно такого определения всех коэффициентов иллюстрируется следующим выражением диссипативной функции, которое оно принимает при выборе одной из осей координат (оси г) вдоль направления ш

2R = 2тп (о_аР — ~y b^vy^ ^[65] -f r\₂vla + 2n₃wL + 2r)₄o_2Zt>_aa +

') Диссипативные коэффициенты нематиков были введены (в другом виде)

+ ri5i&+4-fa + ^X^ (^а«^гЯ + т^h2» (^[66]»^[67])

где индексы а, р\ у пробегают два значения х, у. Поскольку должно быть R > О (энтропия возрастает), то коэффициенты (fli> 42. мз» Не» ^хи» ^х±> У положительны и, кроме того,

Ш5>г\1 (41,6)

Таким образом, нематическая среда характеризуется всего девятью кинетическими коэффициентами: пятью коэффициентами вязкости, двумя коэффициентами теплопроводности, коэффициен­том v (тоже имеющим размерность вязкости) и бездиссипативным безразмерным коэффициентом А..

Число фигурирующих в уравнениях движения коэффициентов вязкости уменьшается в важном случае, когда движущуюся жид­кость можно считать несжимаемой (для чего ее скорость должна быть мала по сравнению со скоростью звука). Уравнение непре­рывности несжимаемой жидкости сводится к равенству div v = = vu — 0. В тензоре напряжений (41,4) второй член выпадает вовсе, а третий принимает вид const. b_ih (nin_mVi_m). Замечаем, что последний член не дает вклада в диссипативную функцию (он выпадает при образовании произведения о«и«, поскольку 1>,д.6,й =» — ^vkh — 0)- Кроме того, он имеет такую же тензорную структуру, как и член —pb_lk в полном тензоре напряжений a_ik. Между тем, в гидродинамике несжимаемой жидкости давление выступает (наряду со скоростью) просто как одна из неизвестных функций координат и времени, определяемых в результате решения урав­нений движения; оно не является здесь термодинамической вели­чиной, связанной с другими подобными величинами уравнением состояния. Поэтому члены —pb_ik и const b_ik (п_гп_ту_гт) в тензоре напряжений можно объединить друг с другом, что сводится просто к переопределению давления. Таким образом, вязкий тензор напряжений несжимаемой нематической жидкости сводится к вы­ражению

Он = 2x\iv_ik + (Лз — 2m) (nitiiVki -f- n_kniVu) -f-

+ (Л₂ + Hi - 2т]₃) щщщпггр_lmi (41,7)

(где f}₂= Лг + 45—2т]₄) и содержит всего три независимых коэф­фициента вязкости. Соответствующая диссипативная функция (ось г вдоль п):

2R = 2ТЦ (v_a& — -j- 6ajSf_w)² + f[₂V% + 2пзУа₂ +

+ ±.\ъ(д_аТГ + х_±(д*ТГ}+-у Л⁸ (41,8)

(напомним, что v_aa + v_zz = 0); положительность коэффициента t]₂ обеспечивается неравенством (41,6).

Задача

Определить силу, действующую на прямолинейную дисклинацию (о индек­сом Франка п = 1), движущуюся в перпендикулярном ее оси направлении (Н. Imura, К. Okano, 1973).

Решение. Рассматриваем дисклинацию в системе координат, где она покоится (и совпадает с осью г), а жидкость движется с постоянной скоростью v вдоль оси х. Распределение п (г) в дисклинации в этой системе стационарно и дается формулами (для дисклинации с радиальными «линиями тока директора», рис. 27, а)

п_х = cos <р, п_у = sin ф,

где полярный угол ф = arctg (у/х). В уравнении (40,3) имеем daldt = 0 и = 0 (ввиду однородности потока),.так что остается

да h дх y

Отсюда находим для возникающего в результате движения слабого молекуляр-ного поля

где v — единичный, вектор в направлении оси г (в отсутствие движения молеку­лярное поле h = 0, так как неподвижная дисклинация представляет собой рав­новесное состояние среды). Диссипативная функция

(х* + у*)*

Энергия, диссипируемая в единицу времени (и отнесенная к единице длины линии дисклинации), дается интегралом

J

2R dx dy = n-pPL, L = In (R/a),

где R — поперечные размеры области движения, а а — молекулярные размеры. Эта Диссипация должна компенсироваться работой of, совершаемой действующей на дисклинацию силой f. Отсюда находим

Для дисклинации с круговыми линиями тока (см, рис, 27, б) получается такой же результат,

§ 42, Распространение малых колебаний в нематиках

Полная система точных уравнений гидродинамики нематиков очень сложна. Она, естественно, упрощается в случае малых "коле­баний, когда допустима линеаризация уравнений.

Приступая к исследованию распространения малых колебаний
в нематических средах, напомним предварительно, какие типы
(моды) колебаний существуют в обычных жидкостях. Прежде всего,
это обычные звуковые волны с законом дисперсии (связью между
частотой со и волновым вектором к) ю = ck и скоростью распро-
странения

^г^^~₍₄₂₎1)

Колебания в звуковой волне продольны (см. VI, § 64).

Далее, существуют сильно, затухающие вязкие волны с зако­ном дисперсии

Дата добавления: 2014-11-07