Ol — V2X 38 страница

Ван-дер-ваальсовой теории критической точки отвечают значения индексов, приведенных в примечании на стр. 528 для теории Ландау.

[56]При t ~ т)^в аргумент функции f (х) в (153,6): х <*> t/t¹^⁶-^ 1, поскольку фактически число (56 = ($ + 7 > 1. Этим доказывается, что в уравнении состояния (153,7) действительно возможен случай t^>p.

[57]Напомним, что под Ф подразумевается здесь (как и в § 149) сингулярная часть термодинамического потенциала. Представляя собой малую поправку к основной, несингулярной, части, она в то же время дает такую же поправку и к другим термодинамическим потенциалам. Отметим, что на кривой фазового равновесия характерная величина этой добавки со г^а~^а (это замечание будет использовано в § 154).

^х) Добавление же в эффективный гамильтониан члена ~ i\³t не нарушило бы его симметрии, так как такой член мог бы быть исключен просто преобра­зованием вида г)—j-r)+const-<. Снова напомним в этой связи (ср. примечание на стр. 534), что в эффективном гамильтониане г) является лишь переменной континуального интегрирования, и поэтому указанное преобразование не меняет статистического интеграла.

^х) Добавление же в эффективный гамильтониан члена ~ i\³t не нарушило бы его симметрии, так как такой член мог бы быть исключен просто преобра­зованием вида г)—j-r)+const-<. Снова напомним в этой связи (ср. примечание на стр. 534), что в эффективном гамильтониане г) является лишь переменной континуального интегрирования, и поэтому указанное преобразование не меняет статистического интеграла.

^х) Добавление же в эффективный гамильтониан члена ~ i\³t не нарушило бы его симметрии, так как такой член мог бы быть исключен просто преобра­зованием вида г)—j-r)+const-<. Снова напомним в этой связи (ср. примечание на стр. 534), что в эффективном гамильтониане г) является лишь переменной континуального интегрирования, и поэтому указанное преобразование не меняет статистического интеграла.

^[61]) Уже упоминалось, что фактически (5 + Y > 1. Неравенство 1— а > р"

^х) Следует иметь в виду, что описываемый механизм образования новой фазы может реально осуществляться лишь в достаточно чистом веществе. На практике же центрами образования новой фазы обычно являются всякого рода загрязнения — пылинки, ионы и т.п.

^[63]) Расчет вероятности возникновения зародышей произвольной величины, демонстрирующий описанные соотношения,—см. задачу 2.

У^г

Ьу ■

Из условия же

находим и^гуЧ6* ~ Др/р. Исключив у из обоих полученных соотношений, на­ходим окончательно:

§ 41. Устойчивость движения в ламинарном пограничном слое

Ламинарное движение в пограничном слое, как и всякое дру­гое ламинарное течение, при достаточно больших числах Рей­нольдса становится в той или иной степени неустойчивым. Ха­рактер потери устойчивости в пограничном слое аналогичен по­тере устойчивости при течении по трубе (§ 28).

Число Рейнольдса для течения в пограничном слое меняется вдоль поверхности обтекаемого тела. Так, при обтекании пла­стинки можно определить число Рейнольдса как R* = Ux/v, где х—расстояние от переднего края пластинки, U — скорость жид­кости вне пограничного слоя. Более характерным для погранич­ного слоя, однако, является такое определение, в котором роль размеров играет какая-либо длина, непосредственно характе­ризующая толщину слоя; в качестве таковой можно выбрать толщину вытеснения, определенную согласно (39,26):

R» = -^¹=l,72 VR,

(41,1)

(числовой коэффициент относится к пограничному слою на пло­ской поверхности).

Ввиду сравнительной медленности изменения толщины слоя с расстоянием, и малости поперечной скорости жидкости в нем, при исследовании устойчивости течения в небольшом участке пограничного слоя можно рассматривать плоско-параллельное течение с неизменным вдоль оси х профилем¹). Тогда с матема-

') При таком рассмотрении остается, конечно, в стороне вопрос о влия­нии, которое может иметь на устойчивость пограничного слоя кривизна обте­каемой поверхности. Имеется также и определенная непоследовательность, связанная с делаемыми пренебрежениями. Дело в том, что единственными плоско-параллельными течениями (с профилем скорости, зависящим только от одной координаты), удовлетворяющими уравнению Навье—Стокса, яв­ляются течения с линейным (17,1) и параболическим (17,4) профилями (в то время как уравнение Эйлера удовлетворяется плоско-параллельным течением с произвольным профилем). Поэтому рассматриваемое в теории устойчивости пограничного слоя основное течение не является, строго говоря, решением уравнений движения.

тической точки зрения задача будет аналогична задаче об устойчивости течения между двумя параллельными плоскостями (о которой шла речь в § 29). Разница состоит лишь в форме профиля скоростей: вместо симметричного профиля с v = 0 на обеих границах здесь имеется несимметричный профиль, в ко­тором скорость меняется от нуля на поверхности тела до задан­ного значения U — скорости потока вне пограничного слоя. Та­кое исследование приводит к следующим результатам (W. Toll-mien, 1929; Н. Schlichting, 1933; С. С. Lin, 1945).

Форма нейтральной кривой на диаграмме со, R (см. § 28) за­висит от формы профиля скоростей в пограничном слое. Если профиль скоростей не имеет точки перегиба (скорость v_x моно­тонно возрастает, причем кривая v_x = v_x(y) везде выпуклая; рис. 28,а), то граница устойчивости имеет форму, вполне анало­гичную той, которая характеризует устойчивость течения в трубе: имеется некоторое минимальное значение R = R_Kp, при кото­ром появляются усиливающиеся возмущения, а при R ->- оо обе ветви кривой асимптотически приближаются к оси абсцисс (рис. 29, а). Для профиля скоростей, имеющего место в погра­ничном слое на плоской пластинке, вычисление дает для крити­ческого значения числа Рейнольдса значение¹) R_eKp«* 420.

Профиль скоростей типа рис. 28, а не может иметь места, если скорость жидкости вне пограничного слоя уменьшается вниз по течению; в этом случае профиль скоростей непременно должен иметь точку перегиба. Действительно, рассмотрим не­большой участок поверхности стенки, который можно считать плоским, и пусть х есть опять продольная координата вдоль на­правления течения, а у — расстояние от стенки. Из соотношения

1 dp ₌ ц 6U р dx дх

(40,10)

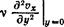
видно, что если U падает вниз по течению (д.1//дх <0), то вблизи поверхности

т. е. кривая v_x = v_x(y) — вогнутая. При увеличении же у ско­рость v_x должна асимптотически приближаться к конечному пре­делу U. Уже из геометрических соображений ясно, что для этого кривая должна стать выпуклой, а потому имеет где-то точку пе­региба (рис. 28,6).

*) При Rj->oo на ветвях I я II нейтральной кривой ю обращается в нуль соответственно как Rj^1/2 и Rjj"¹'⁵. Точке R =я R_Kp отвечает частота <л«р = 0,15- U/6* и волновое число Акр «= 0,36/6*,

При наличии точки перегиба в профиле скоростей форма кривой границы устойчивости несколько меняется. Именно, обе

ния —см. примечание на с. 150). Для меньших значений R, а также для профилей скорости с точкой перегиба вопрос остает­ся открытым.

Благодаря изменению числа Рейнольдса вдоль пограничного слоя, турбулизируется не сразу весь слой, а лишь та его часть, для которой R_e превышает определенное значение. При заданной скорости обтекания это значит, что турбулизация возникает на определенном расстоянии от переднего края; при увеличении скорости это место приближается к переднему краю. Экспери­ментальные данные показывают, что место возникновения тур­булентности в пограничном слое существенно зависит также от интенсивности возмущений в натекающем потоке. По мере умень­шения степени возмущенности наступление турбулентности ото­двигается к более высоким значениям R_e.

Различие между нейтральными кривыми на рис. 29, а и 29, б имеет принципиальный характер. Тот факт, что на верхней вет­ви частота стремится при R_e-»-oo к отличному от нуля пределу, означает, что движение остается неустойчивым при сколь угодно малой вязкости, между тем как в случае кривой типа рис. 23, а при v->-0 возмущения с любой конечной частотой затухают. Это различие обусловлено именно наличием или отсутствием точки перегиба в профиле скоростей v_x = v(y). Его происхождение можно проследить с математической точки зрения, рассмотрев задачу об устойчивости в рамках гидродинамики идеальной жидкости (Rayleigh, 1880).

Подставим в уравнение плоского движения идеальной жид­кости (10,10) функцию тока в виде

Ф = М«/) + *М*> 2/. *),

где 1р₀ — функция тока невозмущенного течения (так что ty'₀ = v(y)), a \pi — малое возмущение. Последнее ищем в виде

tp, = ф (#) _е

Подстановка в (10,10) приводит к следующему линеаризован­ному уравнению для функции tpi'):

(f - j) (Ф" - fe²<p) - 0"<Р = 0. (41,2)

Если границей движения (по оси у) является твердая стенка, то на ней ф = 0 (как следствие условия v_y = 0); если же ши­рина потока не ограничена (с одной или с обоих сторон), то такое же условие должно быть поставлено на бесконечности, где поток однороден. Будем рассматривать k как заданную веще­ственную величину; частота же ш определяется тогда по соб­ственным значениям граничной задачи для уравнения (41,2).

') Любая функция vf>₀(i/) удовлетворяет уравнению (10,10) тождественно}

ср. сказанное в примечании на с. 236.

Разделим уравнение (41,2) на (v — a/k), умножим на <р* и проинтегрируем по у между двумя границами движения yi и у₂. Проинтегрировав произведение ф*ср" по частям, получим

J* (IФ' I² + А²1_Ф I²) dy + J* -£±2L. dy = 0. (41,3)

Первый член здесь во всяком случае веществен. Предполагая частоту комплексной и отделив мнимую часть равенства, полу­чим:

Г У* „. |₂

Для того чтобы могло быть 1таф0, должен обращаться в нуль интеграл, а для этого во всяком случае необходимо, чтобы где-либо в области интегрирования v" проходило через нуль. Таким образом, неустойчивость может возникнуть (при v = 0) лишь для профилей скорости с точкой перегиба ').

С физической точки зрения, происхождение этой неустойчи­вости связано с «резонансным» взаимодействием между колеба­ниями среды и движением ее частиц в основном течении, и в этом смысле оно аналогично происхождению известного из кине­тической теории затухания (или усиления в неустойчивом слу­чае) Ландау колебаний в бесстолкновительной плазме (см. X, § 30)²).

*) Следует отметить, что постановка задачи об устойчивости с точным равенством v = 0 физически не вполне корректна. Она не учитывает того факта, что реальная жидкость непременно обладает хотя бы и малой, но отличной от нуля вязкостью. Это приводит к ряду математических затрудне­ний: исчезновению некоторых решений (в виду понижения порядка диффе­ренциального уравнения для функции <р) и появлению новых решений, отсут­ствующих при v ф 0. Последнее обстоятельство связано с сингулярностью уравнения (41,2) (отсутствующей при V"?*=0): в точке, где v(g) = to/ft, об­ращается в нуль коэффициент при старшей производной в уравнении. ²) Эта аналогия указана А В. Тимофеевым (1979) и А А Андроновым и А Л. Фабрикантом (1979); ниже мы следуем изложению А. В. Тимофеева. ⁸) При v"(y) шг 0 уравнение (41,2) вообще не имеет решений, удовле­творяющих необходимым граничным условиям.

Согласно уравнению (41,2) собственные колебания течения (если они существуют) связаны с той его частью, где и"(у)фО³). Проследить за механизмом усиления колебаний удобно на при­мере профиля скорости, в котором «источник» колебаний лока­лизован в одном слое течения: рассмотрим профиль v(y), кри­визна которого мала везде, за исключением лишь окрестности некоторой точки у = у₀; заменив ее просто изломом профиля; будем иметь в V' (у) член вида А6(у — г/о); именно он будет да­вать основной вклад в интеграл в уравнении (41,3). Будем опи­сывать течение в системе координат, в которой «источник» по-

коится, т. е. v(yo) = 0 (как это изображено на рис. 30). Отде­лив в уравнении (41,3) вещественную часть, получим

\ у Ф-?+#\_фыу ^iff'**-о.

Пусть А > 0 (как на рис. 30); поскольку первый член в этом равенстве заведомо положителен, то тогда должно быть Re u>/k > 0 — фазовая скорость волны направ­лена направо. При этом резонансная точка у_г, в которой фазовая скорость волны совпадает с местной скоростью течения, v(y,) = Re со/А, лежит справа от точки уо- Жидкие частицы, движущиеся в окрестности резонансной точки и обгоняющие волну, отдают ей энергию; ча­стицы же, отстающие от волны, отбирают от нее энергию; волна будет усиливаться (не- р_ис. зо устойчивость), если первых частиц больше чем вторых¹). Но ввиду предполагаемой несжимаемости жидкости число частиц, приходящихся на элемент dy ширины потока, просто пропорционально dy; тем самым число частиц со скоростями в интервале do пропорционально dy — (dy/dv) dv = = dv/v'{y), т. е. роль функции распределения по скоростям иг­рает \/v (у). Следовательно, для возникновения неустойчивости необходимо, чтобы при пересечении точки у, слева направо функ­ция l/v'(y) возрастала, т. е. v'(y) убывала. Другими словами, должно быть v"(yr)<Z0, а поскольку в точке уо производная v" положительна, то где-либо между точками у₀ и у, должна быть точка перегиба профиля.

Аналогичным образом рассматривается (и приводит к тому же результату) случай, когда А < 0; при этом фазовая скорость волны и скорость резонансных жидких частиц направлены на­лево.

§ 42. Логарифмический профиль скоростей

') По отношению к резонансным частицам движение в волне стационар­но; поэтому обмен энергией между ними и волной не обращается в нуль при усреднении по времени (как это имеет место для других частиц, по отноше­нию к которым движение в волне осциллирует). Отметим также, что указан­ное направление обмена энергией отвечает стремлению к уменьшению гради­ента скорости течения, и в этом смысле отвечает учету сколь угодно малой вязкости.

Рассмотрим плоско-параллельный турбулентный поток жид­кости, текущий вдоль неограниченной плоской поверхности (ког­да мы говорим о плоско-параллельности турбулентного, потока, то подразумевается, конечно, усредненное по времени движение в нем)¹). Выберем направление потока в качестве оси х, пло­скость стенки — в качестве плоскости х; г, так что у есть рас­стояние от стенки. Компоненты средней скорости вдоль осей у и г равны нулю: и_х = и, и_у = и_г = 0. Перепад давления отсут­ствует; все величины зависят только от у.

Обозначим посредством в силу трения, действующую на еди­ницу поверхности стенки (и направленную, очевидно, по оси х). Величина а представляет собой не что иное, как импульс, пере­даваемый жидкостью твердой стенке; она является в то же вре­мя тем постоянным потоком импульса (точнее х-компоненты им­пульса), который направлен в отрицательном направлении оси у, и определяет количество импульса, непрерывно передаваемого от более удаленных от стенки слоев жидкости к менее удален­ным.

Наличие этого потока импульса связано, конечно, с нали­чием вдоль оси у градиента средней скорости и. Если бы жид­кость двигалась везде с одинаковой скоростью, то никакого по­тока импульса в ней не было бы. Можно поставить вопрос и обратным образом: зададимся некоторым определенным значе­нием а и выясним, каково должно быть движение в жидкости данной плотности р, приводящее к потоку импульса а. Имея в виду получить асимптотические законы,, относящиеся к очень большим числам Рейнольдса, снова исходим из предположения, что в этих законах не должна фигурировать в явном виде вяз­кость жидкости v (она становится, однако, существенной на очень малых расстояниях у — см. ниже).

Таким образом, значение градиента скорости du/dy на каж­дом расстоянии от стенки должно определяться постоянными параметрами р, а и, разумеется, самим расстоянием у. Един­ственной комбинацией требуемой размерности, которую можно составить из р, а и у, является (а/р)^1/2/у. Поэтому должно быть

—.(42,1)

где введена удобная для дальнейшего величина о. (с размер­ностью скорости) согласно определению

or = pw², (42,2)

а у, — числовая постоянная (постоянная Кармана). Значение к не может быть вычислено теоретически и должно быть опреде­лено из эксперимента. Оно оказывается равным ^я)

________________ к = 0,4. (42,3)

') Излагаемые в §§ 42—44 результаты принадлежат Т. Карману (1930J и Л. Прандтлю (1932).

^а) Это значение (и значение еще одной постоянной в-формуле (42,8) ниже) получено из результатов измерений профиля скорости вблизи стеной труб и прямоугольных каналов и в пограничном слое на плоских стенках.

Интегрируя соотношение (42,1), получим:

«—J-flny+ c), (42,4)

где с — постоянная интегрирования. Для определения этой по­стоянной нельзя воспользоваться обычными граничными усло­виями на поверхности стенки: при у = 0 первый член в (42,4), обращается в бесконечность. Причина этого заключается в том, что написанное выражение становится в действительности не­применимым на очень малых расстояниях от стенки, поскольку при очень малых у влияние вязкости делается существенным и им нельзя пренебрегать. Условия на бесконечности тоже отсут­ствуют: при у = оо выражение (42,4) тоже делается бесконеч­ным. Это связано с тем, что в поставленных нами идеализиро­ванных условиях задачи фигурирует бесконечная поверхность стенки, влияние которой простирается поэтому и на бесконечно большие расстояния.

Прежде чем определить постоянную с, укажем предваритель­но на следующую существенную особенность рассматриваемого движения: оно не имеет никаких характерных постоянных пара­метров длины, которые могли бы определить масштаб турбу­лентного движения, как это имеет место в обычных случаях. По­этому основной масштаб турбулентности определяется самим расстоянием у: турбулентное движение на расстоянии у от стен­ки имеет основной масштаб порядка величины у. Что же ка­сается пульсационной скорости турбулентного движения, то она — порядка величины v». Это тоже следует непосредственно из соображений размерности, поскольку и.— единственная ве­личина с размерностью скорости, которую можно составить из имеющихся в нашем распоряжении величин о, р, у. Подчеркнем, что в то время как средняя скорость падает с уменьшением у, порядок величины пульсационной скорости оказывается одина­ковым на всех расстояниях от стенки. Этот результат находится в согласии с общим правилом, что порядок величины пульса­ционной скорости определяется изменением Аи средней скорости (§ 33). В рассматриваемом случае нет характерных длин /, на которых можно было бы брать изменение средней скорости; Дц должно быть теперь разумным образом определено, как измене­ние и при изменении расстояния у на величину порядка его самого. Но при таком изменении у скорость и меняется согласно (42,4) как раз на величину порядка и».

На достаточно малых расстояниях от стенки начинает играть роль вязкость жидкости; обозначим порядок величины этих рас­стояний посредством уо. Определить уо можно следующим обра­зом. Масштаб турбулентного движения на этих расстояниях — порядка уо, а скорость — порядка и». Поэтому число Рейнольдса, характеризующее движение на расстояниях ~j/₀, есть R ~а

~ yov»/v. Вязкость начинает играть роль при R ~ 1. Отсюда на­ходим, что

Уо ~ v/i/„ (42,5)

чем и определяется интересующее нас расстояние.

На расстояниях у -с у₀ движение жидкости определяется обычным вязким трением. Распределение скоростей здесь может быть получено прямо из обычной формулы для вязкого трения:

du

откуда

u = — y = ~y. (42,6)

Таким образом, непосредственно к стенке прилегает тонкая про­слойка жидкости, в которой средняя скорость меняется по ли­нейному закону. Величина скорости во всей этой прослойке мала — она меняется от нуля на самой стенке до значений ~ и» при у ~ у₀. Эту прослойку называют вязким подслоем. Никакой сколько-нибудь резкой границы между вязким подслоем и ос­тальным потоком, конечно, нет; в этом смысле понятие о вязком подслое имеет лишь качественный характер Подчеркнем, что и в нем движение жидкости турбулентно¹).

В дальнейшем движением в вязком подслое мы не будем интересоваться вовсе. Наличие его надо учесть только соответ­ствующим выбором постоянной интегрирования в (42,4): она должна быть выбрана так, чтобы было и ~ и» на расстояниях у ~ у₀. Для этого надо положить с = —In у₀, так что

и = ^Мп-^. (42,7)

Эта формула определяет (при ограниченных у) распределение¹ скоростей в турбулентном потоке, текущем вдоль твердой стен­ки. Такое распределение называют логарифмическим профилем скоростей²).

') В этом смысле все еще иногда применяемое название «ламинарного подслоя» не адекватно. Сходство с ламинарным движением заключается только в том, что средняя скорость распределена пб такому же закону, по которому была бы распределена истинная скорость при ламинарном движе­нии в тех же условиях. Пульсационное движение в вязком подслое обнаруживает своеобразные особенности, не имеющие еще адекватной теоретической интерпретации. ²) Изложенный простой вывод логарифмического профиля дан Л. Д. Лан­дау (1944).

В формуле (42,7) под знаком логарифма должен был бы на самом деле стоять еще некоторый числовой коэффициент. В написанном виде она имеет, как говорят, лишь логарифмиче­скую точность Это значит, что аргумент логарифма предпола­гается настолько большим, что и сам логарифм велик. Введе­ние небольшого численного коэффициента под знаком логариф­ма в (42,7) эквивалентно прибавлению к написанному выраже­нию дополнительного члена вида const-и», где const — число по­рядка единицы; в логарифмическом приближении таким членом пренебрегается по сравнению с членом, содержащим большой логарифм. Фактически, однако, аргумент логарифма в рассмат­риваемых здесь и ниже формулах все же не очень велик, а по­тому и точность логарифмического приближения не высока. Точ­ность этих формул можно повысить, вводя эмпирический чис­ленный множитель в аргумент логарифма, или, что то же са­мое, прибавляя к логарифму эмпирическую постоянную. Так, более точная формула для профиля скоростей имеет вид:

и = v, (2,5 In -12s. + 5,1) = 2,5i>. In. (42,8)

Отметим, что обе формулы (42,6) и (42,8) имеют вид:

и = 1>,/(|), l = yv₄/v, (42,9)

где f(l) — универсальная функция. Это — прямое следствие того, что | — единственная безразмерная комбинация, которую можно составить из имеющихся в нашем распоряжении параметров р, a, v и переменной у. По этой причине такого рода зависимость должна иметь место на всех вообще расстояниях от стенки, в том числе в области, промежуточной между областями примени­мости формул (42,6) и (42,8). На рис. 31 приведен график функ­ции /(£) в полулогарифмическом (десятичном) масштабе. Сплош­ные линии 1 и 2 отвечают соответственно формулам (42,6) и (42,8); штриховая кривая — эмпирическая зависимость в проме­жуточной области (она простирается примерно от | л; 5 до I «30).

Легко определить диссипацию энергии в рассматриваемом турбулентном потоке. Величина а представляет собой среднее значение компоненты Т1_ху тензора плотности потока импульса. Вне вязкого подслоя в tl_xe можно опустить член с вязкостью, так что U_xy = pv_xv_y. Введя пульсационную скорость v' и помня, что средняя скорость направлена по оси х, имеем v_x = и + v'_x> v_y = v'_y. Тогда¹)

° = f>(»_x*y) = P«»y)+ Р"<»;> = Р<"Х>- (42,10)

') Тензор потока импульса, переносимого турбулентными пульсациями, называют тензором рейнольдсовых напряжений; это понятие было введено Рейнольдсом (О. Reynolds, 1896).

Далее, плотность потока энергии в направлении оси у равна (р + pv²/2)v_y (здесь тоже опущен вязкий член). Написав

V²— (и -f- v'_x)²-h v'_y²-\- V* и усреднив все выражение, получим

<рч>+f +°;³+«#»;>+р«к°;>-

Здесь достаточно сохранить только последний член. Дело в том, что пульсационная скорость — порядка величины о, и потому

Л

f1 Г 1

i i

ft

i

1 ю ' ю^г to* ю*5

Дата добавления: 2014-11-07