Ol — V2X 39 страница

Рис. 31

(с логарифмической точностью) мала по сравнению с и. Что ка­сается давления, то его турбулентные пульсации p^r ~ ро² и по­тому с той же точностью первый член в написанном выражении тоже может быть опущен. Таким образом, находим для средней плотности потока энергии:

(₄) = pu(v'_xv_y) = uo. (42,11)

По мере приближения к поверхности стенки этот поток умень­шается, что связано как раз с диссипацией энергии. Производ­ная d(q)/dy дает диссипацию в единице объема жидкости, а разделив ее на р, получим диссипацию в единице массы:

е = —= —(-). (42,12)

До сих пор мы предполагали, что поверхность сгенки доста­точно гладкая. Если же поверхность шероховата, то выведенные формулы могут несколько измениться. В качестве меры шерохо­ватости стенки можно выбрать порядок величины выступов ше­роховатости, которые мы обозначим посредством d. Существен­на сравнительная величина d и толщина подслоя у₀. Если тол­щина уо велика по сравнению с d, то шероховатость вообще не существенна; это и подразумевается под достаточной гладкостью стенки. Если у₀ и d одного порядка величины, то никаких общих формул написать нельзя.

В обратном же предельном случае сильной шероховатости
(d» уо) снова можно установить некоторые общие соотноше-
ния. Говорить о вязком подслое в этом случае, очевидно, нельзя.
Вокруг выступов шероховатости будет происходить турбулент-
ное движение, характеризующееся величинами р, о, d; вязкость
v, как обычно, не должна входить явно. Скорость этого движе-
ния — порядка величины v_t — единственной имеющейся в нашем
распоряжении величины с размерностью скорости. Таким обра-
зом, мы видим, что в потоке, текущем вдоль шероховатой по-
верхности, скорость делается малой на расстояниях у ~ d
вместо у ~ уо, как это было при течении вдоль гладкой поверх-
ности. Отсюда ясно, что распределение скоростей будет опреде-
ляться формулой, получающейся из (42,7) заменой v/u* на d,

" ⁼ 1Г^,П " <⁴²>¹³>

§ 43. Турбулентное течение в трубах

Применим теперь полученные результаты к турбулентному течению жидкости по трубе. Вблизи стенок трубы (на расстоя­ниях, малых по сравнению с ее радиусом а) ее поверхность можно приближенно рассматривать как плоскую и распределение ско­ростей должно описываться формулой (42,7) или (42,8). Од­нако ввиду медленного изменения функции In у можно с лога­рифмической точностью применить формулу (42,7) и к средней скорости U течения жидкости в трубе, написав в этой формуле вместо у радиус а трубы:

t/-^lnib.. (43,1)

Под скоростью U мы будем подразумевать количество (объем) жидкости, протекающей в 1 с через сечение трубы, деленное на площадь этого сечения: U = Q/pna².

Для того чтобы связать скорость U с поддерживающим тече­ние перепадом давления Ар/1 (Ар — разность давлений на кон­цах трубы с длиной /), замечаем следующее. Действующая на все сечение потока жидкости в трубе движущая сила есть па²Ар. Эта сила идет на преодоление трения о стенки. Поскольку отнесенная к единице площади стенки сила трения есть а = pv* то полная сила трения равна 2nalpv\. Приравнивая оба выра­жения, находим:

4^= Р^1- (43,2)

Уравнения (43,1) и (43,2) определяют в параметрическом виде (параметром является и») связь скорости течения жидкости по трубе с перепадом давления в ней. Об этой связи говорят обычно как о законе сопротивления трубы. Выражая к» через Ар/1 из (43,2) и подставляя в (43,1), получаем закон сопротивления в виде уравнения

"-VH^vVlr⁷)- («л

Обычно в этой формуле вводят так называемый коэффициент сопротивления трубы, являющийся безразмерной величиной и определяющийся как отношение

^~UW' (43.4)

Зависимость X от безразмерного числа Рейнольдса R = 2aU/v определяется неявным образом уравнением

-j= = 0,88 In (RV^)- 0,85. (43,5)

Мы поставили здесь для и значение (42,3) и прибавили к ло­гарифму эмпирическую численную постоянную¹). Определяе­мый этой формулой коэффициент сопротивления является мед­ленно убывающей функцией числа Рейнольдса. Для сравнения приведем закон сопротивления при ламинарном течении в трубе. Вводя в формулу (17,10) коэффициент сопротивления, получаем:

X = 64/R. (43,6)

При ламинарном течении коэффициент сопротивления падает с ростом числа Рейнольдса быстрее, чем при турбулентном те­чении.

') Коэффициент перед логарифмом в этой формуле взят в соответствии с коэффициентом в формуле (42,8) логарифмического профиля скоростей. Только при таком условии эта формула имеет теоретический смысл предельной формулы для турбулентного течения при достаточно больших значениях чис­ла Рейнольдса. Если же выбирать в формуле (43,5) произвольным образом значение обеих входящих в нее постоянных, то она сможет играть роль лишь чисто эмпирической формулы для зависимости X от R. В таком случае, одна­ко, нет никаких оснований предпочитать ее любой другой, более простой, эмпирической формуле, достаточно хорошо описывающей экспериментальные данные.

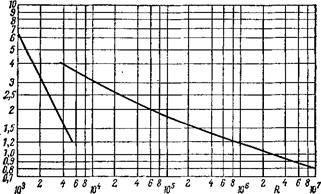
На рис. 32 изображен (в логарифмическом масштабе) график зависимости X от R. Круто спадающая прямая соответствует ла­минарному режиму (формула (43,6)), а более полотая кривая

турбулентный пограничный слой

(практически тоже близкая к прямой) — турбулентному течению. Переход с первой на вторую происходит по мере увеличения числа Рейнольдса в момент турбулизации течения, который мо­жет наступить при различных значениях R в зависимости от конкретных условий течения (от степени «возмущенности» по­тока); в момент перехода коэффициент сопротивления резко возрастает.

Ркс. 32

Написанные выше формулы относятся к трубам с гладкими стенками. Аналогичные формулы для труб с сильно шерохова­тыми стенками получаются просто заменойv/v* на d (ср. (42,13)). Для закона сопротивления получим теперь вместо (43,3) фор­мулу

^Vw'"f <⁴³>⁷>

Под знаком логарифма стоит теперь постоянная величина, не
содержащая перепада давления, как это было в (43,3). Мы ви-
дим, что средняя скорость течения теперь просто пропорцио-
нальна квадратному корню из градиента давления в трубе. Если
ввести коэффициент сопротивления, то формула (43,7) примет
вид ₂ ^

^{Л =} In² (aid) ⁼ In² (aid) ' (^43,8)

т. е. Я — постоянная величина, не зависящая от числа Рей­нольдса.

§ 44. Турбулентный пограничный слой

Тот факт, что мы получили для плоско-параллельного тур­булентного потока логарифмический закон распределения ско­ростей формально во всем пространстве, связан с тем, что рас­сматривалось течение вдоль стенки, площадь которой беско­нечна. При течении же вдоль поверхности реальных конечных тел логарифмическим профилем обладает лишь движение на не­больших расстояниях от поверхности — в пограничном слое.

Толщина пограничного слоя растет вниз по течению вдоль обтекаемой поверхности (закон этого возрастания будет найден ниже). Это объясняет, почему при течении по трубе логариф­мический профиль имеет место вдоль всего сечения трубы. Тол­щина пограничного слоя у стенки трубы растет, начиная от вхо­да в трубу. Уже на некотором конечном расстоянии от входа по­граничный слой как бы заполняет собой все сечение трубы. По­этому если рассматривать трубу как достаточно длинную и не интересоваться ее начальным участком, то течение во всем ее объеме будет того же типа, как. и в турбулентном пограничном слое. Напомним, что аналогичное положение имеет место и для ламинарного течения по трубе. Оно всегда описывается форму­лой (17,9); роль вязкости в нем проявляется на всех расстояниях от стенки и никогда не бывает ограничена тонким пристеноч­ным слоем жидкости.

Падение средней скорости как в турбулентном, так и в ла­минарном пограничном слое, обусловливается в конечном итоге вязкостью жидкости. Однако влияние вязкости проявляется в турбулентном пограничном слое очень своеобразно. Самый ход изменения средней скорости в слое не зависит непосредственно от вязкости; вязкость входит в выражение для градиента ско­рости только в вязком подслое. Общая же толщина погранич­ного слоя определяется вязкостью и обращается в нуль вместе с ней (см. ниже). Если бы вязкость была в точности равна нулю, то никакого пограничного слоя вовсе не было бы.

Применим полученные в предыдущем параграфе результаты к турбулентному пограничному слою, образующемуся при обте­кании тонкой плоской пластинки, — таком же, какое было рас­смотрено в § 39 для ламинарного течения. На границе турбу­лентного слоя скорость жидкости почти равна скорости U основ­ного потока. С другой стороны, для определения этой скорости на границе мы можем (с логарифмической точностью) восполь­зоваться формулой (42,7), подставив в нее вместо у толщину пограничного слоя б¹). Сравнив оба выражения, получим:

£/ = ^-lni£. (44,1)

Здесь U играет роль постоянного параметра; толщина же б ме­няется вдоль пластинки, а вместе с ней является, следовательно,

') Фактически логарифмический профиль наблюдается не на всей тол-' щине пограничного слоя. Последние 20—25 % набора скорости на его наруж­ной стороне происходят быстрее, чем по логарифмическому закону. Эти от­клонения связаны, по-видимому, с нерегулярными колебаниями границы слоя (ср. сказанное в конце § 35 о границах турбулентных областей).

медленно меняющейся функцией от л; и величина и«. Для опре­деления этих функций формула (44,1) недостаточна; необходимо получить еще какое-нибудь соотношение, которое бы связывало v* и б с х.

Для этого воспользуемся теми же соображениями, с помощью которых была получена формула (37,3) для ширины турбулент­ного следа. Как и там, производная db/dx должна быть порядка величины отношения скорости вдоль оси у на границе слоя к скорости вдоль оси х на той же границе. Вторая из них — по­рядка U, что же касается поперечной скорости, то она обя­зана пульсационному движению и потому — порядка о*. Таким образом,

db v.

откуда

6--^. (44,2)

Формулы (44,1) и (44,2) определяют вместе зависимость и» и б от расстояния х¹). Эта зависимость, однако, не может быть написана в явном виде. Ниже мы выразим 6 через некоторую вспомогательную величину. Но поскольку и» есть медленно ме­няющаяся функция от х, то уже из (44,2) видно, что толщина слоя меняется в основном пропорционально х. Напомним, что толщина ламинарного пограничного слоя растет как х^1/2, т. е. медленнее, чем в турбулентном слое.

Определим зависимость от х силы трения а, действующей на единицу площади поверхности пластинки. Эта зависимость опре­деляется двумя формулами:

v v²x a = pv²„ t/^-Mn-^.

Вторая из них получается подстановкой (44,2) в (44,1) и обла­дает логарифмической точностью. Введем коэффициент сопро­тивления с (отнесенный к единице площади поверхности пла­стинки), определяемый как безразмерное отношение

Тогда, исключая у» из двух написанных уравнений, получим следующее уравнение, определяющее (с логарифмической точ­ностью) в неявном виде зависимость с от х:

л^=\псЪ_х, R, = -^-. (44,4)

') Строго говоря, расстояние д: должно отсчитываться примерно от места перехода ламинарного слоя в турбулентный.

Определяемый этой формулой коэффициент сопротивления с яв­ляется медленно убывающей функцией расстояния х.

Через эту функцию можно выразить толщину пограничного слоя. Имеем:

Подставив это в (44,2), находим:

б = const • jc V^е • (44,5)

Эмпирическое значение коэффициента в этой формуле — около 0,3.

Аналогичным образом можно получить формулы для турбу­лентного пограничного слоя на шероховатой поверхности. Со­гласно формуле (42,13), имеем теперь вместо (44,1):

и d

где d — размеры выступов шероховатости. Подставив сюда б из (44,2), получим:

^и у. ¹¹¹ Ud '

или, введя сюда коэффициент сопротивления (44,3):

'5T_,„£iL. ₍44,б)

§ 45. Кризис сопротивления

Из полученных в последних параграфах результатов можно сделать существенные заключения о законе сопротивления при больших числах Рейнольдса, т. е. о зависимости действующей на обтекаемое тело силы сопротивления от R при больших значе­ниях последнего.

Картина обтекания при больших R (о которых только и идет речь ниже) выглядит, как уже говорилось, следующим образом. Во всем основном объеме жидкости (т. е. везде, за исключением пограничного слоя, которым мы здесь не интересуемся) жид­кость может рассматриваться как идеальная, причем ее движе­ние является потенциальным везде, кроме области турбулентного следа. Размеры — ширина — следа зависят от положения линии отрыва на поверхности обтекаемого тела. При этом существен­но, что хотя это положение и определяется свойствами погра­ничного слоя, но в результате оказывается, как было отмечено в § 40, не зависящим от числа Рейнольдса. Таким образом, мы можем сказать, что вся картина обтекания при больших числах Рейнольдса практически не зависит от вязкости, т. е., другими

словами, от R (до тех пор, пока пограничный слой остается ла­минарным; см. ниже).

Отсюда следует, что и сила сопротивления не может зависеть от вязкости. В нашем распоряжении остаются только три вели­чины: скорость U натекающего потока, плотность жидкости р и размеры тела I. Из них можно составить всего лишь одну величину с размерностью силы; pl!²l². Вместо квадрата линей­ных размеров тела введем, как это обычно делают, пропорцио­нальную ему площадь 5 поперечного (по отношению к направ­лению обтекания) сечения тела и напишем:

F = const-p(/²S, (45,1)

где const — численная постоянная, зависящая только от формы тела. Таким образом, сила сопротивления должна быть (при больших R) пропорциональна площади сечения тела и квадрату скорости обтекания. Напомним для сравнения, что при совсем малых R(R<1) сопротивление было пропорционально первой степени линейных размеров тела и первой степени скорости (F ~ vplU; см. § 20)¹).

Обычно, как уже говорилось, вместо силы сопротивления F рассматривают коэффициент сопротивления С, определяемый как

С= ^F

С является безразмерной величиной и может зависеть только от R. Формула (45,1) напишется в виде

С = const, (45,2)

т. е. коэффициент сопротивления зависит только от формы тела.

Такой ход силы сопротивления не может, однако, продол­жаться до сколь угодно больших чисел Рейнольдса. Дело в том, что при достаточно больших R ламинарный пограничный слой (на поверхности тела до линии отрыва) делается неустойчивым и турбулизуется. При этом турбулизуется не весь пограничный слой, а лишь некоторая его часть. Вся поверхность тела может быть разделена, таким образом, на три части: на передней имеется ламинарный пограничный слой, затем идет область тур­булентного слоя и, наконец, область за линией отрыва.

Турбулизация пограничного слоя существенно сказывается на всей картине течения в основном потоке: она приводит к замет­ному смещению линии отрыва вниз по течению жидкости, так что турбулентный след за телом сужается (как это изображено

') Своеобразный случай, когда сопротивление остается пропорциональ­ным первой степени скорости при больших значениях R, — обтекание пузырь­ка газа; см. задачу к этому параграфу.

схематически на рис. 33; область следа заштрихована)¹). Суже­ние турбулентного следа приводит к уменьшению силы сопротив­ления. Таким образом, турбулизация пограничного слоя при больших числах Рейнольдса сопровождается падением коэффи­циента сопротивления. Коэффициент сопротивления падает в не­сколько раз в сравнительно узком интервале чисел Рейнольдса (в области R, равных нескольким 10⁵). Это явление называется

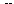
3 1,5 1,0 0,6 0,3

^с х^-
						г-

10"

o,i 1 г 5 w ю^г' w^J

Рис. 34

кризисом сопротивления. Уменьшение коэффициента сопротивле­ния настолько значительно, что само сопротивление, которое при постоянном С должно возрастать пропорционально квадрату скорости, в этой области чисел Рейнольдса Даже убывает с воз­растанием скорости²).

') Так, при поперечном обтекании длинного цилиндра турбулизация по­граничного слоя сдвигает положение точки отрыва от 95 до 60° (угвл на окружности сечения цилиндра отсчитывается от направления обтекания). ²) Отметим, что первое возникновение нестационарности при обтекании шара (при R порядка нескольких десятков) не сопровождается скачкообраз­ным изменением силы сопротивления. Это связано с непрерывностью-перехода при мягком самовозбуждении. Изменение характера течения могло бы про­явиться лишь в появлении излома на кривой C(R),

Можно отметить, что на явление кризиса влияет степень тур­булентности набегающего на тело потока. Чем она больше, тем раньше (при меньших R) наступает турбулизация пограничного слоя. В связи с этим и падение коэффициента сопротивления на­чинается при меньших числах Рейнольдса (и растягивается по более широкому интервалу их значений).

На рис. 34 и 35 приведен экспериментально найденный гра­фик зависимости коэффициента сопротивления*от числа Рей­нольдса R = Ud/v для шара диаметра d (на рис. 34 — в лога­рифмическом, а на рис. 35 — в обыкновенном масштабе). При самых малых R (R «С 1) коэффициент сопротивления падает по закону C = 24/R (формула Стокса). Падение С продолжается затем более медленно вплоть до R «5-Ю³, где С достигает ми­нимума, вслед за чем несколько повышается. В области чисел Рейнольдса 2-Ю⁴— 2-Ю⁵ имеет место закон (45,2), т. е. С прак­тически остается постоянным. При R«2v3'10^s наступает кризис со­противления, причем коэффициент сопротивления падает примерно в 4—5 раз.

Для сравнения приведем пример обтекания, при котором не происхо­дит явления кризиса. Рассмотрим обтекание плоского диска в направ­лении, перпендикулярном к его пло­скости. Место отрыва в этом случае заранее очевидно из чисто геоме­трических соображений, — ясно, что отрыв произойдет по краю диска и в дальнейшем уже никуда не бу­дет смещаться. Поэтому при увеличении R коэффициент со­противления диска остается постоянным, не обнаруживая кри­зиса.

Следует иметь в виду, что при тех больших скоростях, когда наступает кризис сопротивления, может уже стать заметным влияние сжимаемости жидкости. Параметром, характеризующим степень этого влияния, является число М = U/c, где с — ско­рость звука; жидкость можно рассматривать как несжимаемую, если М< 1 (§ 10). Поскольку из двух чисел М и R лишь одно содержит размеры тела, то эти числа могут меняться независи­мо друг от друга.

Экспериментальные данные свидетельствуют о том, что ежи- • маемость оказывает в общем стабилизующее влияние на дви­жение в ламинарном пограничном слое. При возрастании числа М увеличивается критическое значепие R, при котором происхо­дит турбулизация пограничного слоя. В связи с этим отодви­гается также и наступление кризиса сопротивления. Так, для шара при изменении М от 0,3 до 0,7 кризис сопротивления ото-двигается примерно от R «4-10⁵ до 8-10⁵.

Укажем также, что при увеличении М положение точки от­рыва в ламинарном пограничном слое смещается вверх по те­чению — по направлению к переднему концу тела, что должно приводить к некоторому увеличению сопротивления.

Задача

Определить силу сопротивления, действующую на движущийся в жид­кости газовый пузырек при больших числах Рейнольдса.

»„ = -т,$-

Решение. На границе жидкости с газом должна обращаться в нуль не самая касательная составляющая скорости жидкости, а лишь ее нормаль­ная производная (вязкостью газа пренебрегаем.) Поэтому градиент скорости вблизи поверхности не будет аномально велик, пограничный слой (в том виде, о котором шла речь в § 39) будет отсутствовать, а потому будет отсутство­вать (почти по всей поверхности пузырька) также и явление отрыва. При вы­числении диссипации энергии с помощью объемного интеграла (16,3) можно поэтому во всем пространстве пользоваться распределением скоростей, соот­ветствующим потенциальному обтеканию шара (задача 2 § 10), пренебрегая при этом ролью поверхностного слоя жидкости и очень тонкого турбулент­ного следа. Производя вычисление по формуле, полученной в задаче к § 16, найдем

dv²

2nR² sin 9 dQ = — l2nr\RU\

дг

Отсюда видно, что искомая диссипативная сила сопротивления

F= l2nr\RU.

Область применимости этой формулы фактически невелика, так как при достаточном увеличении скорости пузырек теряет свою сферическую форму.

§ 46. Хорошо обтекаемые тела

Можно поставить вопрос о том, какова должна быть форма тела (при заданной, например, площади его сечения) для того, чтобы оно испытывало при движении в жидкости по возмож­ности малое сопротивление. Из всего предыдущего ясно, что для этого во всяком случае необходимо достичь по возможности бо­лее позднего отрыва: отрыв должен произойти поближе к зад­нему концу тела так, чтобы турбулентный след был как можно более узким. Мы уже знаем, что возникновение отрыва облег­чается наличием быстрого возрастания давления вдоль обтекае­мого тела вниз по течению Поэтому необходимо придать телу такую форму, чтобы изменение давления вдоль него, — в той области, где давление возрастает, происходило по возможности медленно и плавно. Этого можно достичь приданием телу удли­ненной (в направлении обтекания) формы, причем оно плавно заостряется в направлении обтекания так, что стекающие с раз­ных сторон поверхности тела потоки как бы плавно смыкаются без того, чтобы им пришлось где-либо обтекать какие-нибудь углы или же сильно поворачивать по отношению к направлению набегающего потока. Спереди же тело должно быть закруглено; при наличии здесь угла скорость жидкости на его краю обрати­лась бы в бесконечность (см. задачу 6 § 10), вслед за чем про­изошли бы сильное возрастание давления вниз по течению и неизбежный отрыв.

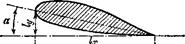
Всем этим требованиям в высокой степени удовлетворяют формы типа, изображенного на рис. 36. Изображенный на ниж-

нем рисунке профиль может представлять собой сечение удли­ненного тела вращения, но может быть и сечением тела с боль­шим размахом (о таких телах мы будем условно говорить как о крыльях). Профиль сечения крыла может быть и не симмет­ричным, как, например, на верхнем рис. 36. При обтекании тел такой формы отрыв происходит лишь в непосредственной бли­зости острого конца, в результате чего коэффициент сопротив­ления достигает относи­тельно малых значений. Такие тела называют хо­рошо обтекаемыми.

В сопротивлении хо­рошо обтекаемых тел за­метную роль играет эф­фект непосредственного трения жидкости о по­верхность в пограничном слое. Этот эффект сравни­тельно очень мал и по­тому практически совершенно несуществен для плохо обтекае­мых тел (о которых шла речь в предыдущем параграфе). В об­ратном же предельном случае обтекания плоской пластинки (па­раллельным ей потоком жидкости) он представляет собой един­ственный источник сопротивления (§ 39).

При обтекании хорошо обтекаемого крыла, наклоненного под малым углом к направлению потока (а на рис. 36, так называе­мый угол атаки), развивается большая подъемная сила F_y, при этом сопротивление Fx остается малым, и в результате отноше­ние Fy/Fx может достичь больших значений (порядка 10—100). Так продолжается, однако, лишь до тех пор, пока угол атаки не сделается слишком большим (обычно ~10). После этого со­противление начинает очень быстро возрастать, а подъемная сила падать. Это явление обусловливается тем, что при боль­ших углах атаки тело перестает удовлетворять условиям хоро­шей обтекаемости: место отрыва сильно смещается по поверх­ности тела по направлению к его переднему краю, в результате чего след делается значительно более широким. Надо иметь в виду, что в предельном случае тела очень малой толщины, т. е. плоской пластинки, хорошее обтекание имеет место только при очень малом угле атаки; отрыв происходит на переднем крае пластинки уже при малых углах ее наклона к направлению потока.

Угол атаки а отсчитывается, по определению, от того поло­жения крыла, при котором подъемная сила равна нулю. При малых углах атаки подъемную силу можно разложить в ряд по степеням а. Ограничиваясь первым членом разложения, мы мо­жем считать силу F_y пропорциональной а. Далее, по тем же со­ображениям размерности, как и для силы сопротивления, подъ­емная сила должна быть пропорциональна pU². Введя также длину размаха 1_г крыла, можно написать:

F_y = const • pU²al_xl₂, (46,1)

i

где const — численная постоянная, зависящая только от формы крыла и не зависящая, в частности, от угла атаки. Для крыльев очень большого размаха можно считать подъемную силу про­порциональной размаху; в этом случае const зависит только от формы профиля поперечного сечения крыла.

Вместо подъемной силы крыла часто пользуются так назы­ваемым коэффициентом подъемной силы, определяемым как

Для крыльев очень большого размаха согласно сказанному выше он пропорционален углу атаки и не зависит ни от скорости движения, ни от размаха крыла:

С_у = const • а. (46,3)

Для вычисления подъемной силы хорошо обтекаемого крыла с помощью формулы Жуковского необходимо определить цирку­ляцию скорости Г. Это делается следующим образом. Везде, кроме области следа, движение потенциально. В данном же слу­чае след очень тонок и занимает на поверхности крыла лишь очень небольшую область вблизи его задней заостренной кром­ки. Поэтому для определения распределения скоростей (а с ним и циркуляции Г) можно решать задачу о потенциальном обте­кании крыла идеальной жидкостью. Наличие следа учитывается при этом тем, что от острой задней кромки крыла отходит по­верхность касательного разрыва, на которой потенциал испыты­вает скачок ф₂ — <Pi = Г. Как было уже показано в § 38, на этой поверхности испытывает скачок также и производная dcp/dz, а производные ду/дх и ду/ду непрерывны. Для крыла конечного размаха поставленная таким образом задача имеет однозначное решение. Нахождение точного решения, однако, весьма сложно.

Если крыло обладает очень большим размахом (и постоян­ным вдоль размаха сечением), то, рассматривая его как беско­нечно длинное вдоль оси г, можно считать движение жидкости плоским (в плоскости х, у). Из соображений симметрии ясно, что при этом скорость Vz — dy/dz в направлении размаха будет вообще равной нулю. В этом случае, следовательно, мы должны искать решение, в котором испытывает скачок только сам по­тенциал при непрерывных его производных; другими словами, поверхность касательного разрыва вообще отсутствует, и мы имеем дело просто с неоднозначной функцией ц>(х,у), прини­мающей конечное приращение Г при обходе по замкнутому кон-

туру, охватывающему обтекаемый профиль. В таком виде, од­нако, задача о плоском обтекании не однозначна, так как допу­скает решение при произвольном, заранее заданном скачке по­тенциала. Для получения однозначного ответа необходимо по­требовать выполнения дополнительного условия (С. А. Чаплы­гин, 1909)

Это условие заключается в требовании, чтобы скорость жид­кости не обращалась в бесконечность на острой задней кромке крыла; напомним в этой связи, что при огибании угла идеаль­ной жидкостью скорость в вершине угла обращается, вообще говоря, в бесконечность по степенному закону (задача 6 § 10). Можно сказать, что поставленное условие означает, что струи, стекающие с обеих сторон крыла, должны плавно смыкаться без того, чтобы поворачивать вокруг острого угла. Естественно, что при выполнении этого условия решение задачи о потенци­альном обтекании приведет к картине, наиболее близкой к ис­тинной, при которой скорость везде конечна, а отрыв происходит лишь у самой задней кромки. Решение становится после этого вполне однозначным и, в частности, определяется и нужная для вычисления подъемной силы циркуляция Г.

Дата добавления: 2014-11-07